[논문번역] GRUI-GAN: Multivariate Time Series Imputation with Generative Adversarial Networks (NeurIPS 2018)
paper: https://arxiv.org/ftp/arxiv/papers/2009/2009.08900.pdf
Abstract
시계열 데이터에는 결측치가 많고 이는 여러 분석들을 방해한다. mean/zero imputation, case deletion, matrix factorization imputation등과 같은 접근은 시간적인 의존성과 복잡한 분포의 성질을 무시한다.
이 논문에서는 데이터 생성으로 결측치 imputation을 다룬다.
이미지 생성에서의 Generative Adversarial Networks(GAN)의 성공에 영감을 받아서, 우리는 다변수의 시계열 데이터의 전체적인 분포를 GAN을 이용해서 학습하는 것을 제안한다.
이미지 데이터와 다른 점은 시계열 데이터는 보통 데이터 측정 과정의 특성 때문에 불완전하다는 점이다.
시계열의 불완전한 시간적 불규칙성을 표현하기 위해 수정된 Gate Recurrent Unit(GRU)가 GAN안에 구현되어 있다.
실험의 결과 제안된 모델과 간단한 모델이 state-of-the-art의 결과를 가지고 있는 것을 확인했다.
Introduction
결측치를 처리하는 것은 매우매우 중요하다.
최근에 랜덤 노이즈 로부터 진짜 sample을 만들 수 있는 GAN이 소개 됐다. GAN은 사람 얼굴 완성과 문장생성에서 성공적으로 적용됐다. 그러나 얼굴을 완성하거나 문장을 생성하기 전에, 이러한 방법들은 우리의 경우에는 없는 완벽한 훈련 데이터셋을 필요로한다. 또한 GAN을 결측치 대체에 사용하는 연구는 매우 적다.
GAN의 이미지 imputation에서의 성공에 영감을 받아서, 우리는 불완전한 시계열 데이터를 생성하고 보간하기 위해 adversarial model의 장점을 가져왔다.
불규칙적인 시간 간격의 관측들의 잠재된 관계를 학습하기 위해서, 고정되지 않은 시간 간격을 고려하고 시간 간격에 의해 결정된 과거의 관측을 희미하게 하기 위해서 GRUI라는 새로운 RNN cell을 제안한다.
첫번째 단계에서는, GRUI를 GAN의 discriminator와 generator로 채택해서, 잘 훈련된 adversarial model은 전체 데이터셋의 분포와 관측과 데이터셋의 시간적 정보사이의 숨겨진 관계에 대해 학습할 수 있다.
두번째 단계에서는, 우리는 생성된 시계열이 가능한 원래의 불완전한 데이터와 가깝고, 생성된 데이터의 실제일 확률이 가장 크도록 GAN의 generator의 입력 “noise”를 훈련한다.
우리가 아는 바로는, 이것은 adversarial network를 시계열 보간에 사용한 첫번째 연구이다. 우리는 우리의 모델을 실제 의학 데이터셋과 기상 데이터 셋에서 평가해보았다. 그 결과는 imputation 정확도 측면해서 baseline들에 비해 우리의 접근이 더 좋은 것을 보여줬다. 우리의 모델은 prediction과 imputed datasets을 이용한 regression에서도 좋은 결과를 보여줬다.
Method
다변수의 시계열데이터는 다음과 같이 주어진다.
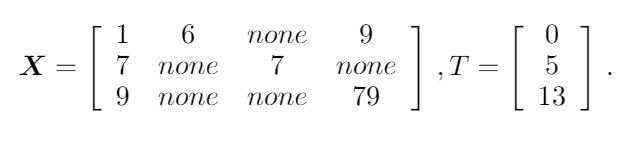
4개의 변수가 3개의 time step으로 주어진 예시이고, none이 결측치이다.
시계열 X가 불완전하면, 우리는 M이라는 mask matrix를 사용한다. mask matrix는 값이 있으면 1, 없으면 0인 값을 가지는 matrix이다.
시계열 데이터에서 결측치를 합리적인 값으로 대체하기 위해서, 우리는 먼저 원래 시계열 데이터셋의 분포를 학습하는 GAN based model을 훈련했다.
이 custom GAN model에서는, 랜덤 벡터로부터 가짜 시계열을 생성하는 generator와 진짜 데이터와 가짜 데이터를 구분하는 discriminator가, generator의 표현 능력을 증가시키는 것 뿐만 아니라 discriminator의 구별하는 능력을 강화하는 능력도 평형을 얻어낼 것이다.
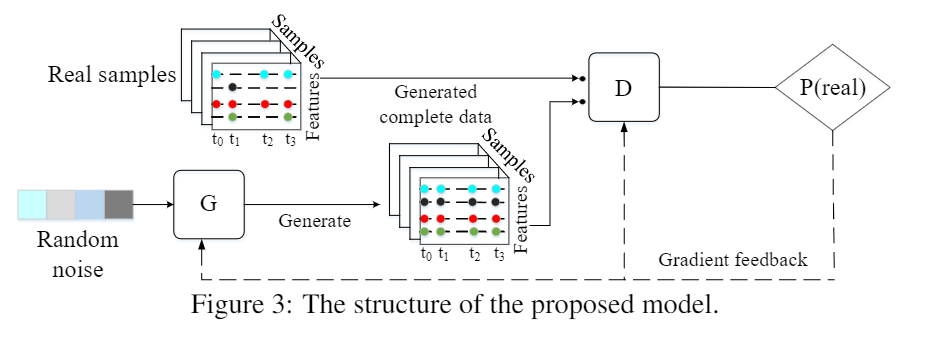
다음에 우리는 네트워크의 구조를 수정하고 generator의 입력 랜덤 벡터를 최적화하여 생성된 가짜 시계열이 결측치를 가장 잘 데체할 수 있도록 한다.
다음 section에서 GAN architecture의 세부적인 부분을 보여주고, 그 다음에 결측치를 impute하는 방법에 대해 설명한다.
GAN architecture
GAN은 gernerator(G)와 discriminator(D)로 만들어진다. G는 랜덤 노이즈 벡터 z를 실제 데이터로 바꾸는 G(z)의 mapping을 학습한다. D는 인풋 데이터가 진짜인 확률을 알려주는 D(.)의 매핑을 찾는다.
D의 인풋은 진짜지만 불완전한 샘플들과 G에 의해 생성된 가짜지만 완전한샘플들이 포함된다는 것에 주목해야 한다. 왜냐하면 mode collapse problem 때문에 전통적인 GAN 은 훈련하기 힘들다.
WGAN은 더 쉽게 훈련하기 위해 Wasserstein distance를 사용한 GAN의 또다른 훈련 방법이다. WGAN은 mode collapse 문제에서 벗어나고 GAN 모델을 최적화하기 쉽게 만들어서 학습 단계의 안정성을 증가시킬 수 있다.
우리의 방법에서는 우리는 WGAN을 전통적인 GAN보다 선호한다. WGAN의 loss function은 다음과 같다.
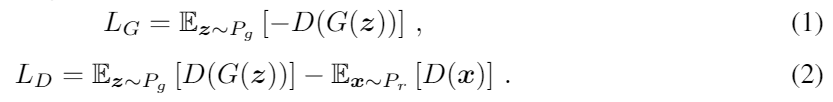
우리가 GAN의 구조를 디자인할때 우리는 G와 D의 기본 네트워크로 state-of-the-art RNN cell인 GRU를 채택했다. LSTM과 같은 다른 RNN들도 사용이 가능하다.
하지만 데이터의 불완전성으로 인해 두개의 연속된 관측사이의 시간 차이가 크다. 그래서 전통적인 GRU나 LSTM은 우리의 시나리오에서 적용이 불가능하다.
불규칙한 시간 간격을 효과적으로 다루고 시간 구간에서의 내제된 정보를 학습하기위해 , 우리는 GRU에 기반한 GRUI cell을 제안한다.
GRUI
원래의 불완전한 시계열 데이터셋의 분포와 특징을 적절히 학습하기 위해, 우리는 “none” 값 때문에 연속한 두개의 관측의 시간간격이 항상 바뀐다는 것을 찾았다. 관측들 사이의 시간 간격들은 알수 없는 불균일한 분포를 따르기 때문에 매우 중요하다. 변할수 있는 시간 간격들이 있다면 우리에게 만약 어떤 변수가 오랫동안 결측됐다면 그 과거 관측의 영향은감쇄 되어야 한다.
과거 관측의 감쇄된 영향을 고려하기 위해, 우리는 불완전한 시계열 데이터의 시간적 불규칙성을 모델링하기 위해 Gated Recurrent Unit for data Imputation (GRUI) cell 을 제안한다.
X의 가까운 존재하는 두 값들의 시간 간격을 기록하기 위해서, 우리는 현재값과 마지막 실제 값 사이의 시간 간격을 기록하는 matrix인 델타를 사용했다. 그 예시는 아래와 같다.
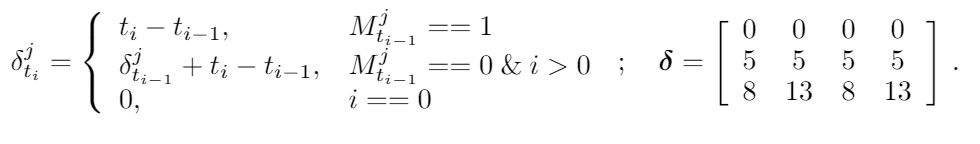
우리는 과거 관측의 영향을 조절하는 시간 decay vector인 베타도 사용했다. 베타의 각 값은 0~1의 값이어야 하고 델타가 커지면 베타는 작아진다. 식으로보면 아래와 같다.

W와 b는 학습해야할 파라미터다. 우리는 베타를 (0,1]로 만들기 위해 음의 exponential을 적용했다. 게다가 델타의 상호작용을 나타내기 위해 W로 대각 matrix 보다는 full weight matrix를 사용했다. decay vector를 얻어낸 후에 우리는 GRU hidden state hti-1 를 decay factor 베타를 element-wise로 곱해서 업데이트 했다. batch normalization을 사용했기 때문에 hidden state h는 1보다 작을 확률이 높다. 우리는 다른 방법 말고 곱셈의 감쇄 방법을 선택했다. GRUI의 업데이트 함수는 다음과 같다.
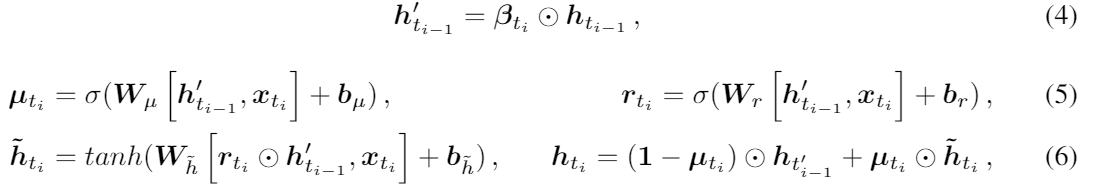
GRU에서 베타가 들어가는거 말고는 다 똑같다.
동그라미 점은 element-wise multiplication이다.
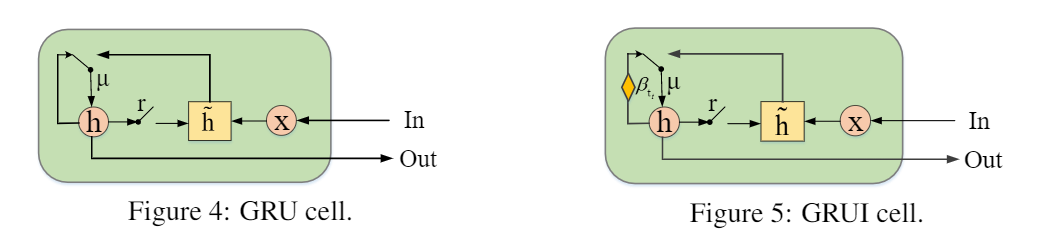
D and G structure
D는 먼저 GRUI layer를 통해 구성돼서 불완전하거나 완전한 시계열을 학습한다. 그리고 FC layer가 GRUI의 마지막 hidden state에 쌓여있다. 오버피팅을 막기위해 우리는 FC layer에 dropout을 적용했다. 우리가 원래의 불완전한 실제의 시계열 데이터를 D에 집어넣었을 때, δ의 한 행의 값은 같지 않다. 하지만 우리가 G에 의해 생성된 가짜 시계열 데이터를 넣어을 때는, 델타의 각행의 값은 같다. (missing value가 없기 때문에 간격이 일정하다.)
우리는 생성된 샘블들의 시간 간격들이 원래의 샘플들과 확실히 같기를 원한다. 그래서 G또한 GRUI layer와 FC layer로 구성되어 있다. G 는 self-feed network이다. 곧, 현재 G의 아웃풋이 다음 반복에서 동일한 cell의 인풋으로 들어간다는 뜻이다.
G의 첫번째 입력은 랜덤 노이즈 벡터 z이고, 가짜 샘플의 델타의 모든 행은 일정한 값이다.
batch normalization은 G와 D모두에 적용되었다.
Missing Values Imputation by GAN
GAN architecture에서, generator G 가 랜덤 노이즈 벡터 z에서 결측치가 없는 완벽한 시계열 데이터로 만드는 G(z) = z -> x 의 mapping을 학습할 수 있다는 것을 알 수 있다.
그러나, 문제는 랜덤 노이즈 벡터 z가 Gaussian 분포와 같은 숨겨진 공간에서 randomly sample되었다는 것이다. 이 말인 즉슨, 생성된 샘플들은 입력 랜덤 노이즈 z가 변하는 거에 따라서 많이 변할 것이다. 생성된 샘플들은 원래의 샘플들의 분포를 따름에도 불구하고, 생성된 샘플들과 원래의 샘플들의 거리 또한 커질 것이다. 즉, x와 G(z)의 유사성의 정도가 충분히 크지 않다.
예를 들어 원래의 불완전한 시계열이 두개의 분류를 포함하고, G는 이 두 분류에 매우 잘 맞는 분포를 학습한다. 주어진 불완전한 샘플 x와 랜덤 인풋 벡터 z에서, G(z)는 x의 반대되는 분류에 속할것이고 이것은 우리가 원하는게 아니다. G(z)가 진짜 분류에 속하더라도 분류 내의 샘플들의 유사성도 클수가 있다.
(뭔 소리지)
어떤 불완전한 시계열 x에 대해서, 생성된 샘플 G(z)가 x와 가장 비슷하도록 가장 좋은 랜덤 노이즈 벡터 z를 잠재 input space 에서 찾아야 한다. 어떻게 결측치를 가장 reasonalble한 값들로 대체할수 있을까?
imputation 의 적합도를 측정하는 방법을 소개한다. 우리는 imputation의 적합도를 평가하기 위해 두 파트의 loss function을 정의했다.
첫번째 파트는 masked reconstruction loss이다. 이것은 생성된 샘플 G(z)가 원래의 불완전한 시계열 x와 충분히 비슷해야한다는 것을 뜻한다. 또 다른 파트는 discriminative loss이다. 이 파트는 생성된 샘플 G(z)를 가능한 실제와 가깝게 만든다. 아래에서 자세히 설명한다.
Masked Recostruction Loss
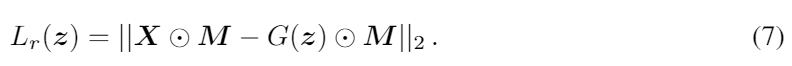
masked reconstruction loss는 원래의 샘플 x와 생성된 샘플 G(z)사이의 mask된 제곱 에러로 정의된다. 우리가 오직 non-missing data에 대해서만 에러를 계산하는 것에 주목해야한다.
Discriminative Loss
discriminative loss은 생성된 샘플 G(z)의 신뢰도를 나타낸다. 이것은 discriminator D의 아웃풋에 기반하여 인풋 샘플 G(z)가 진짜인지에 대한 신뢰 레벨을 나타낸다. 우리는 noise vector z를 G에 넣어서 생성된 샘플 G(z)를 얻고 G(z)를 D에 넣어서 최종적인 discriminative loss 를 얻는다.

Imputation Loss
우리는 랜덤 노이즈 벡터 z를 최적화하기 위해 imputation loss 를 정의했다. imputation loss는 masked reconstruction loss와 discriminative loss의 합이다.
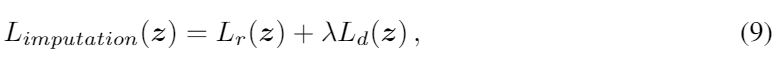
λ는 두 로스 사이의 비율을 조절하는 하이퍼 파라미터이다.
각각의 원래의 시계열 x마다, 우리는 0평균 1분산인 Gaussian distribution에서 랜덤하게 z를 샘플하고 잘 훈련된 generator G에 넣어서 G(z)를 얻는다.
그 다음 noise z를 Limputation으로 훈련하기 시작한다. imputation loss가 최적의 해답에 수렴한 후에, 우리는 x의 결측치를 생성된 G(z)로 아래의 식에서 처럼 대체하면 된다.
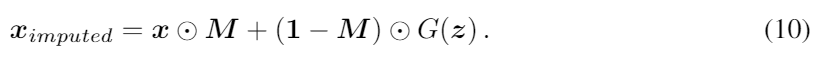
Conclusion
GRU에 decay를 적용한 새로운 모델인 GRUI를 만들고 GAN을 적용해서 데이터를 생성하는 관점으로 결측치를 보간한 방법이다.
결측치를 대체하는 목적으로 GAN을 사용했다는 점이 특징이다.
직접 코드로 구현했을 때는 별로 좋은 결과를 확인하지 못했다.
GAN을 수렴시키는 것은 언제나 어려운것 같다.