[논문번역] NAOMI: Non-AutOregressive Multiresolution sequence Imputation (NeurIPS 2019)

paper: https://arxiv.org/pdf/1901.10946.pdf

code: https://github.com/felixykliu/NAOMI

길이가 긴 결측치를 보간하는 데에 특화된 모델

divide & conquer를 사용하여 긴 길이의 결측치를 나눠서 보간하는 것이 특징.

 

Abstract

결측치 대체는 모션 트래킹 부터 물리적 시스템의 동역학 까지 시공간적인 모델링에서 기본적인 문제이다. Deep autoregressive model 은 긴 범위의 시퀀스를 imputing할 경우 심각한 오류 전파를 겪는다. 이 논문에서는 non-autoregressive 접근과 새로운 deep 생성 모델을 제안한다: Non-AutOregressive Multiresolution Imputation (NAOMI) , 긴 범위의 시퀀스의 임의의 결측 패턴을 대체한다.

NAOMI 는 시공간 데이터의 multiresolution 구조를 이용하고, divide-and-conquer 방법을 사용해서 거친 해상도에서 미세한 해상도 까지 재귀적으로 decode한다.

우리는 adversarial training을 사용하여 우리의 모델을 더욱 발전시켰다. 결정론적 및 확률적인 시스템에서 평가할 때 우리의 실험에서 NAOMI는 imputation 정확도를 크게 증가시켰고, 긴 범위의 시퀀스에 대해서도 일반화했다.

 

Introduction

결측값의 문제는 실생활의 시계열 데이터에서 종종 발생한다. 결측값은 학습 데이터의 관측 편향을 유발하여 학습을 불안정하게 한다. 그런 이유로 결측값을 imputing하는 것은 시퀀스 학습 작업에서 매우 중요하다.

시퀀스 imputation은 수십년동안 통계적인 방법으로 연구되어 왔다. 대부분의 통계적 기술들은 결측 패턴들에 대한 강한 가정들에 의존적이라서 본 적없는 데이터를 일반화하지 못한다. 게다가, 존재하는 방법들은 결측 데이터의 비율이 높고 시퀀스의 길이가 길면 제대로 작동을 하지 않는다.

최근의 연구들은 시퀀스 데이터에서 결측 패턴을 유연하게 학습하기 위해 깊은 생성 모델을 사용해서 제안 되었다. 그러나 존재하는 모든 deep generative imputaion 방법들은 autoregressive이다. 이전 타임 스텝의 값을 이용해서 현재의 타임 스탬프값을 모델링하고 결측 데이터를 순차적으로 impute한다. 그런 이유로 autoregressive 모델들은 복합 에러에 매우 민감하고 긴 범위의 시퀀스 모델링에 치명적일 수 있다. 우리는 우리의 실험에서 기존의 autoregressive 접근방법이 긴 범위의 imputation 작업에서 어려움을 격는 것을 확인했다.

이 논문에서, 우리는 긴 범위의 시퀀스 imputation을 위한 새로운 non-autoregressive 접근을 소개한다. 오직 과거의 값들로 조절하는 것 대신, 우리는 과거의 미래 모두의 조건의 분포를 모델링 한다. 우리는 시공간적 시퀀스의 multiresolution 특징을 사용하고, 복잡한 의존성을 여러개의 resolution에서 더욱 간편하게 분해한다. 우리의 모델은 divide and conquer 전략을 사용하여 결측치를 재귀적으로 채운다. 우리의 방법은 일반적이고 다양한 학습 목적에 사용가능하다.

요약하면, 우리의 기여는 다음과 같다.

• 우리는 긴 범위의 시공간적 시퀀스에서 결측값을 imputing할 수 있는 deep generative 모델의 새로운 non-autoregressive decoding 과정을 제안했다.
• 우리는 분산을 줄이기 위해 fully differentiable generator를 갖는 generative adversarial imitaion learning을 사용한 adversarial training을 소개한다.
• 우리는 교통정보, 당구, 농구 경로를 포함한 시퀀스 데이터셋에 대한 철처한 실험을 진행한다. 우리의 방법은 정확도에서 60%의 증가가 있었고, 주어진 임의의 결측 패턴에서 진짜 시퀀스를 생성했다.

 

Non-Autoregressive Multiresolution Sequence Imputation

X = (x1, x2, …, xT) 를 T관측의 시퀀스라고 한다. X는 masking sequence M = (m1,m2,.., mT)로 표 표현되는 결측치를 가지고 있다. masking mT는 xt가 결측값일 경우 0의 값을 갖는다. 우리의 목표는 결측치를 시퀀스들의 모음에 결측 데이터를 적절한 값으로 대체하는 것이다.

결측값을 imputation하는 보통의 방법은 불완전한 시퀀스들의 분포를 직접 모델링 하는 것이다. 그 예시는 확률을 chain rule을 이용해 분해하고 imputation을 위한 deep autoregressive model을 학습하는 것이 될 수 있다. (GRU-D도 여기에 해당)

그러나 autoregressive 모델들의 주요한 약점은 그들의 순차적 decoding 과정이다. 현재 값이 과거의 time step에 의존하기 때문에, autoregressive 모델은 보통 sub-optimal beam search에 의존해야 하며, 긴 번위의 시퀀스의 에러 compounding에 취약하다.

모델이 알고있는 미래를 참고하지 못하기 때문에 시퀀스 imputation에서 더욱 악화디며, 이는 관측된 지점에서 imputed 값과 실제의 값의 불일치로 이어진다. 이러한 사항들을 완화시키기 위해, 우리는 non-autoregressive 접근방법을 대신 사용하고 deep, non-autoregressive, muliresolution 생성모델인 NAOMI를 제안한다.

 

NAOMI Architecture and Imputation Strategy

아래 그림에서 볼 수 있듯이, NAOMI는 두 개의 요소를 가지고 있다.

1) 불완전한 시퀀스를 hidden representations로 만드는 forward-backward encoder

2) 주어진 hidden representations에서 결측치를 impute하는 multiresolution decoder

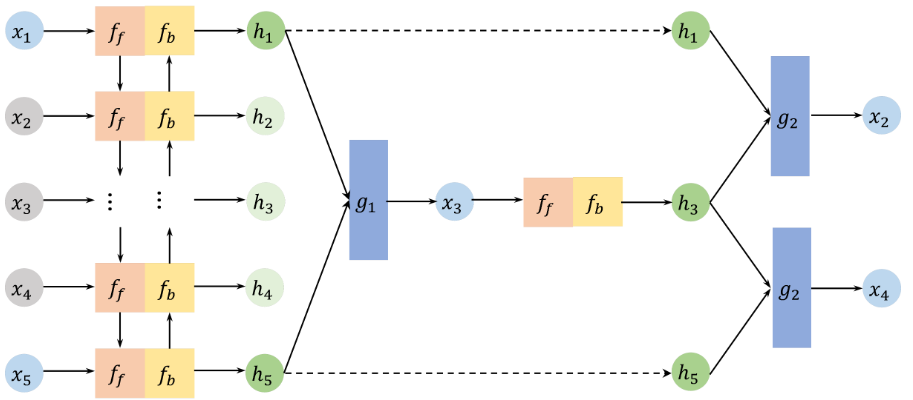
5의 길이의 시퀀스의 imputing에 대한 NAOMI 구조이다. (x2,x3,x4: missing values)

forward-backward encoder는 불완전한 시퀀스 (x1,…,x5)를 hidden states로 인코딩한다.

decoder는 non-autoregressive 방법으로 재귀적으로 디코드한다 : hidden states h1, h5를 이용해서 x3를 예측한다. 그리고 hidden states들은 업데이트된다. 그리고 x2는 x1와 예측된 x3를 이용해서 impute되고 x4도 비슷하게 진행된다. 이러한 과정은 모든 결측치들이 채워질 때까지 반복된다.

 

Forward-backward encoder

우리는 관측과 마스킹 시퀀스를 concatenate 해서 (I = [X,M]) 인풋으로 사용한다. 우리의 인코더 모델은 인풋이 주어졌을 때 두 개의 hidden states의 두 집합의 상태 분포를 모델링 한다.

두 hidden states는 forward hidden states H^f = (h₁^f, …,h_T^f) 와 backward hidden states H^b = (h₁^b, …,h_T^b) 이다.

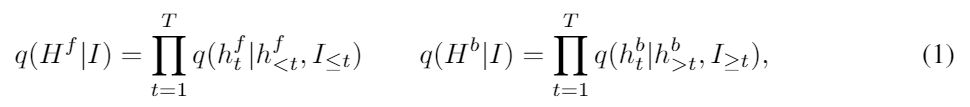
여기서 h_t^f 와 h_t^b는 각각 과거의 미래의 hidden states이다.

우리는 위의 분포를 forward RNN f_f와 backward RNN f_b로 파라미터화 했다.

 

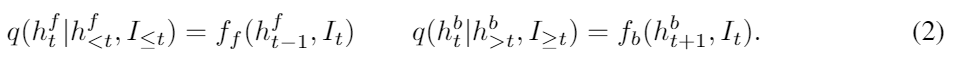
Multiresolution decoder

주어진 joint hidden states H := [H^f, H^b]에 대해서, decoder는 완벽한 문장 p(X|H)의 분포에 대해 학습한다. 우리는 divide and conquer 방법을 적용하고 반복적으로 decode했다.

위의 그림에서처럼, 각각의 반복마다 디코더는 두개의 알려진 타임 스텝을 기준으로 삼는다 (예시에서는 x1,x5). 그리고 그 두 점의 modpoint(x3)를 impute한다. 하나의 기준점은 새롭게 impute된 스텝으로 대체되고 더 세밀한 간격으로 x2, x4에 대해서 과정이 반복된다.

공식적으로 말하면, R resolutions을 가진 디코더는 디코딩 함수의 모음 R개로 구성되어 있고, 각각은 모든 2^R-r 번을 예측한다. 디코더가 처음으로 알려진 스텝 i,j를 기준으로 찾고, 결측 step t를 midpoint에 가깝게 선택한다 [(i+j)/2]. r을 n_r <= (j-i)/2를 만족하는 가장 작은 resolution이라고 하자. 디코더는 hidden tates를 forward states와 backward states를 이용해서 업데이트 한다. 디코딩 함수 g는 hidden states를 아웃풋의 분포로 변환한다.

만약 분포가 deterministic하다면 ,g는 imputed 값을 바로 출력한다. stochastic에서는 g 는 gaussian distribution의 평균과 표준 편차를 출력한다. 그리고 예측은 reparameterize trick을 이용하여 gaussian 분포에서 샘플된다. mask mt는 imputation 된 후에 1로 업데이트 되고, 다음 resolution으로 과정이 진행된다. 위의 알고리즘에서 자세한 과정이 나와있다.

 

Efficient hidden states update

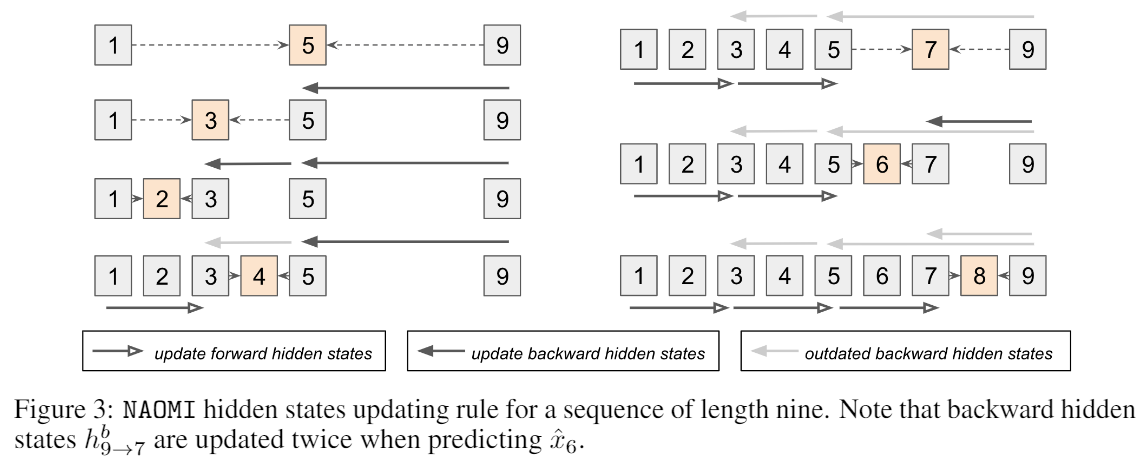
NAOMI는 과거의 연산을 재사용하는 것으로 hidden states를 효과적으로 업데이트한다. 그리고 autoregregressive 모델과 같은 시간 복잡도를 가지고 있다. 아래 그림에서 9 길이의 시퀀스의 예시를 보여준다.

회색 블럭은 알고있는 타임 스텝이고, 오랜지 블럭은 impute할 목표 타임 스텝이다. 회색 화살표는 오래된 hidden states 업데이트 이다. 점선 화살은 디코딩 과정을 나타낸다. 전의 hiddens states들은 imputed 타임 스템에 저장되고 재사용된다. 그러므로 forward hidden states h^f는 오직 한번만 업데이트 되고 backward hidden states h^b는 최대 두번 업데이트 된다.

 

Complexity

NAOMI의 총 런타임은 O(T)이다. 메모리 사용량은 bi-directional RNN (O(T))와 비슷하다. 우리는 오직 forward encoder에 마지막 hidden states만 저장하면 된다. 디코더의 하이퍼 파라미터 R은 2^R이 가장 평범한 결측 구간 사이즈가 가깝도록 설정한다. 그리고 실행시간은 시퀀스 길이의 로그에 비례한다.

 

Learning Objective

C를 완성된 시퀀스의 모임이라고 하고, G(X,M) 은 우리의 생성 모델 NAOMI을 나타내고, p(M)은 사전의 masking을 나타낸다. imputation model은 다음을 최적화하면서 학습된다.

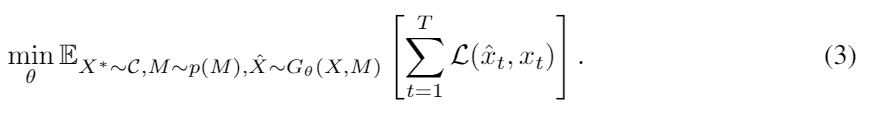
L은 로스 함수이다. deterministic dynamics에서는 로스로 mse를 사용한다. stochastic dynamics에서는 우리는 L을 adversarial 학습을 하는 discriminator로 대체할 수 있다.

 

Adversarial training

gerator G와 discriminator D의 adversarial 학습 최적화 함수는 다음과 같다.

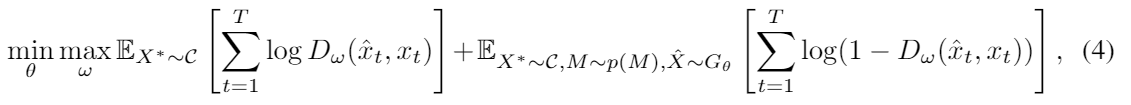
Test

오픈되어 있는 도로 교통 데이터에 자체적으로 데이터를 없애고 이 방법을 직접 적용해 본 결과는 아래와 같다.

파란선이 실제, 노란선이 예측이다.

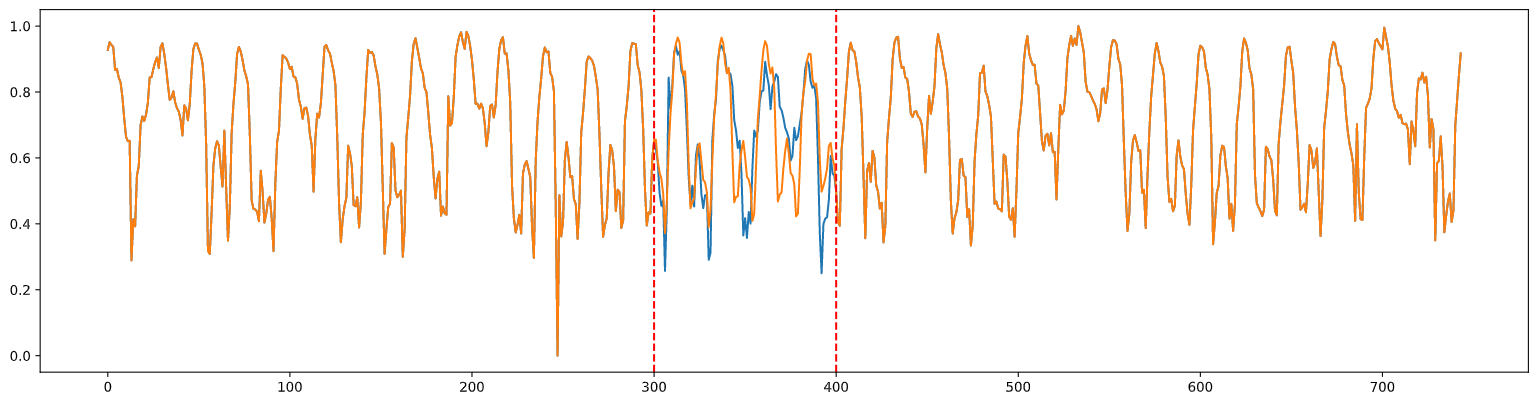
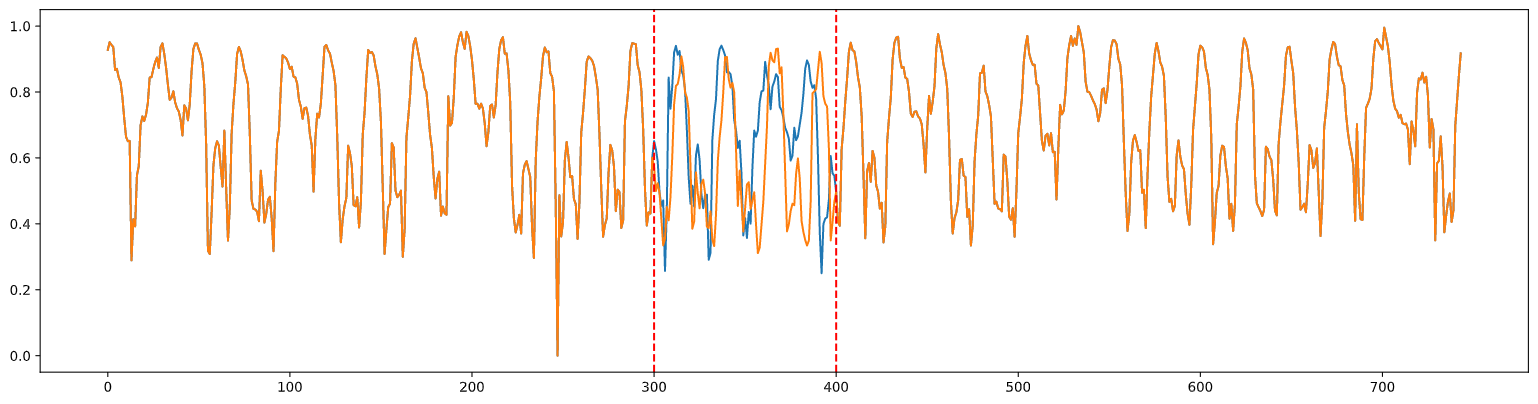
위의 사진은 pretrain만 한 결과고 아래 사진은 GAN까지 적용시킨 결과다.

GAN은 적용시키지 않은게 더 좋은 결과가 나왔으며 나쁘지 않은 성능의 결과를 확인할 수 있다.