[논문번역] GRU-D: Recurrent Neural Networks for Multivariate Time Series with Missing Values (2016)
paper: https://arxiv.org/pdf/1606.01865.pdf
code: https://github.com/zhiyongc/GRU-D
요약: decay rate를 이용하여 결측치를 대체하고, 결측치를 채운 값이라는 표시인 mask를 학습과정에 포함하여 학습을 진행한다.
missing value imputation 자체에 대한 논문이 아니라 missing value가 있는 time series data를 가지고 학습을 하는 방법에 대한 논문.
마지막으로 관측된 값과 절대적인 평균으로 결측치를 대체하므로 헬스 데이터처럼 절대적 평균(ex.체온,맥박, 혈압) 있는 데이터에만 사용이 가능해서 매우 제한적으로만 사용 가능하다.
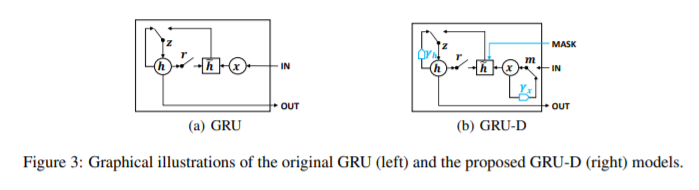
Masking, Time interval을 활용하여 missingvalue에 대한 정보를 얻음
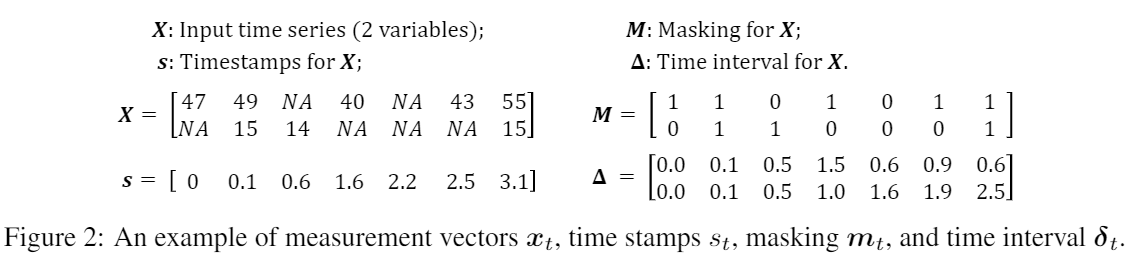
GRU
결측값 처리에 대한 작업은 GRU의 구조에 수정이 없는 3가지 방법으로 해결이 가능하다.
GRU-mean: 결측치가 아닌 값들의 평균을 사용
GRU-forward: 결측치가 아닌 마지막 값을 사용
GRU-simple: 위의 방법으로 구한 값과 결측치 여부를 알려주는 mask와 time interval을 concat해서 사용
=> concat(x, mask, time interval)
이러한 방법들은 결측치가 채워진건지 진짜 관측된 값인지 구분하지 못한다.
단순히 결측치 마스킹과 시간 간격 벡터의 concat으로는 결측치의 시간적 구조를 사용하지 못한다.
따라서 이러한 방법은 결측성을 완벽하게 사용하지 못한다.
̄x
GRU-D
근본적으로 시계열 데이터에서 결측치를 설명하기 위해 헬스 케어 데이터에서 주로 볼 수 있는 두가지 특징을 생각해야한다.
- 결측치의 마지막 관측값이 오래전에 발생한 경우 결측치의 값은 기본값에 가까운 경향이 있다. 이러한 특징은 사람의 몸의 헬스케어 데이터에 주로 존재한다. (항상성과 같은 이유로)
- 인풋 변수가 한동안 누락될 경우 그 변수의 영향은 시간이 지날 수록 희미해진다.
우리는 이러한 특징을 포착할 수 있도록 decay메커니즘이 설계된 GRU기반의 GRU-D라고 불리는 모델을 제안한다.
우리는 decay 메커니즘을 사용하기 위해 앞서 말한 요소들을 구현하는 decay rates를 소개한다.
- 헬스 케어 시계열 데이터에서 각각의 입력 변수는 자신만의 의학적 의미와 중요성을 가지고 있다. decay rates은 변수와 관련된 근본적인 특징에 따라 변수마다 달라야 한다.
- 많은 결측 패턴이 예측 작업에서 유용할 때, decay rate은 그러한 패턴들을 나타내고 예측 작업에 도움을 주어야 한다.
- 결측 패턴은 알려지지 않았고 복잡하기 때문에, 우리는 a priori를 고치기 보다는 decay rates를 학습하는 것을 목표로 한다.
요약: 변수마다 decay rates가 있고 데이터가 시간이 지날 수록 희미해지는 것을 표현한다. 이 값을 학습한다.
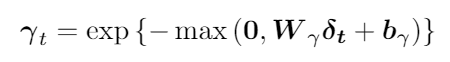
decay rates는 점점 감소하는 0~1의 값을 가진다. sigmoid와 같이 점점 감소하는 0~1사이의 값을 가지는 함수라면 다른걸 사용해도 된다.
GRU-D 모델은 두개의 훈련가능한 decays를 통합하여 입력특징값과 RNN states과 함께 missingness를 utilize한다.
우선 결측치에 대해서, 마지막 관측값을 그대로 사용하는 대신 시간이 지남에 따라 empirical mean (초기 설정에서 얻어올수 있는 상수)을 향해 decay하는 input decay를 사용한다.
이러한 가정하에, 훈련가능한 decay scheme는 다음과 같이 쉽게 적용될 수 있다.
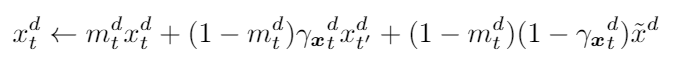
x^d_t’은 d번째 값의 마지막관측값이고 x^~d는 d번째 값의 empirical mean이다.
해석해보면 결측치는 마지막 관측 값과 가깝고 마지막 관측값에서 시간이 지날수록 절대적인 평균에 가까워진다.
결론: 결측치를 impute하는 방법이 위와 같고 감마도 학습 parameter에 포함된다.
이 결과를 gru기반의 gru-d에 넣어서 예측하면 된다.
code example
x = mask * x + (1 - mask) * (delta_x * x_last_obsv + (1 - delta_x) * x_mean)
Conclusion
결측치 대체에 대한 초창기 논문인 것 같다.
체온처럼 항상성이 있는 데이터에 대해서만 사용할 수 있어서 사용하기가 매우 제한적이다.
하지만 이 논문 이후에도 자주 사용되는 요소인 decay를 사용한다는 아이디어를 처음(아마?) 제안했다는 점에서 의미가 있는 것 같다.
구조도 간단해서 조건만 맞다면 사용하기에는 쉬운 모델이다.ㄴ