[코드구현] Time Series Forecasting - ARIMA
한 시간 간격으로 측정 되어 있는 한 달치 특정 구간의 평균 속도 데이터를 이용하여 마지막 일주일 간의 평균 속도를 예측하는 task를 수행해 보았다.
데이터는 도로교통공사의 오픈 데이터를 직접 가공하였으며 아래에서 다운로드할 수 있다.
전통적 통계 모델인 ARIMA (Autoregressive integrated moving average)과 여기에 추가로 계절성을 포함하는 모델인 SARIMAX를 사용하여 예측을 진행했다.
ARIMA의 사용법은 아래의 영상을 참고했다.
Load Data
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
df = pd.read_csv("서인천IC-부평IC 평균속도.csv", encoding='CP949')
df = df.drop(df.columns[0], axis=1)
df.columns = ["ds","y"]
df.head()
| ds | y | |
|---|---|---|
| 0 | 2021050100 | 98.63 |
| 1 | 2021050101 | 100.53 |
| 2 | 2021050102 | 99.86 |
| 3 | 2021050103 | 99.34 |
| 4 | 2021050104 | 93.64 |
데이터를 보면, 첫번째 column에는 년도, 월, 일, 시 가 연속해서 주어져 있고 두 번 째 column에는 평균 속도가 있다.
plt.figure(figsize=(20,5))
plt.plot(range(len(df["ds"])), df["y"])
plt.show()
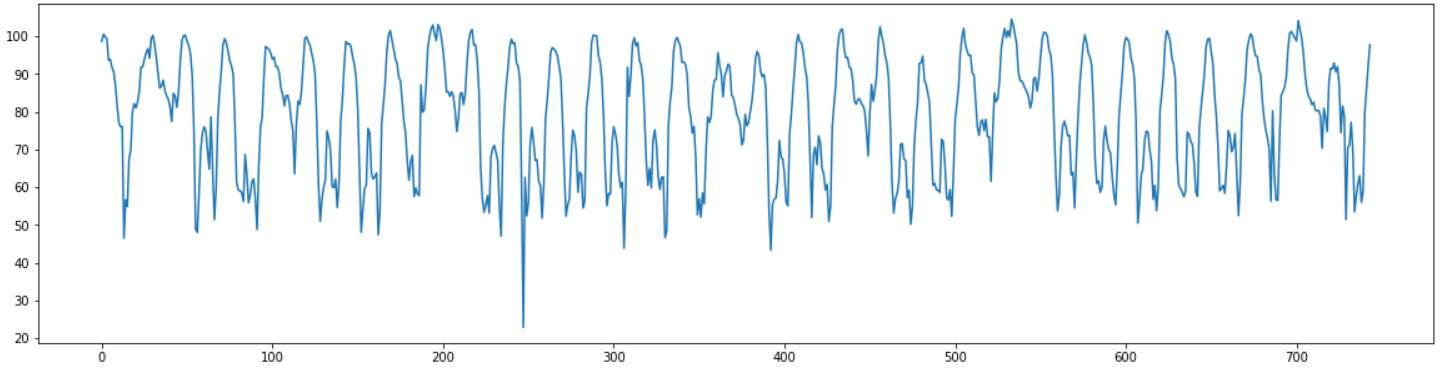
전체 데이터를 살펴보면 744개의 데이터를 가지고 있는 위와 같은 형태를 띄고 있는 것을 확인 할 수 있다.
df_train = df.iloc[:-24*7]
마지막 일주일의 데이터를 예측하는 것이 목표 이므로 마지막 일주일을 제외한 데이터를 훈련 데이터로 설정한다.
Data Analysis
Seasonal Decompose
교통 데이터는 주기를 가지고 있는 데이터인 경우가 많으므로 먼저 seasonal decompose를 진행해 본다.
from statsmodels.tsa.seasonal import seasonal_decompose
result = seasonal_decompose(df_train["y"], model="additive", period=24)
fig = plt.figure()
fig = result.plot()
fig.set_size_inches(20,7)
plt.show()
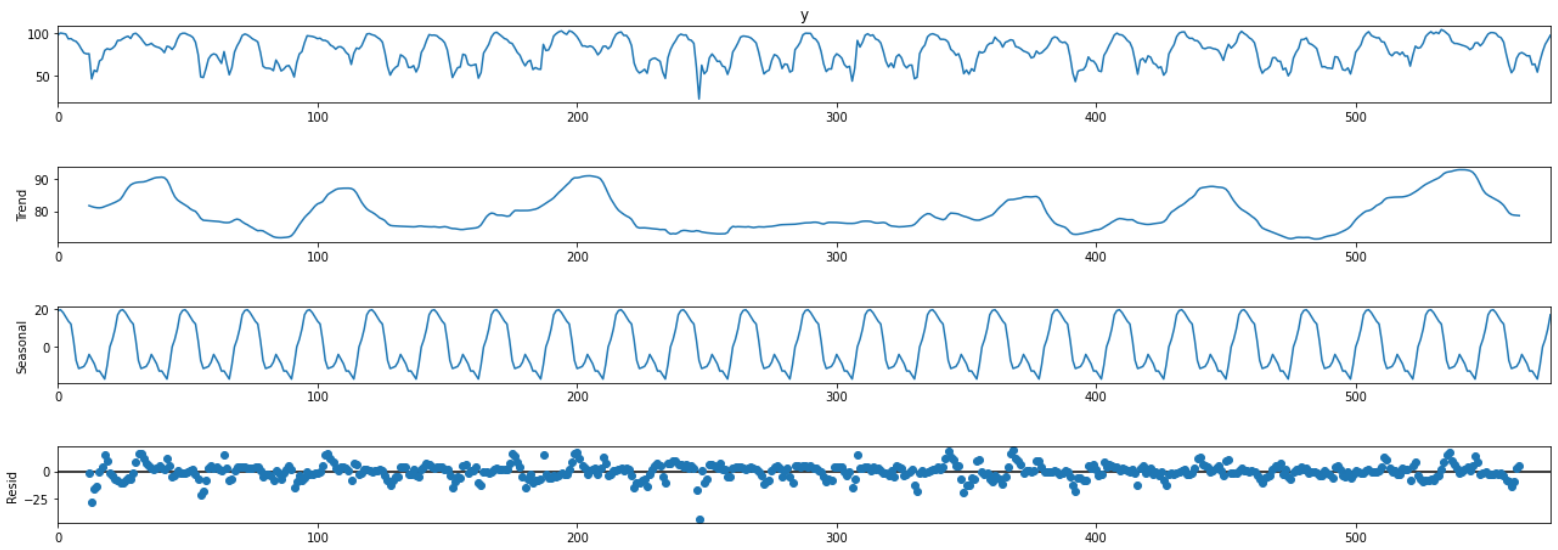
결과를 확인해 보면 명확한 주기성을 가지고 있다는 것을 알 수 있다.
ACF, PACF
ARIMA를 적용하기 전에 먼저acf, pacf를 확인해 본다.
import statsmodels.api as sm
fig = plt.figure(figsize=(20,8))
ax1 = fig.add_subplot(211)
fig = sm.graphics.tsa.plot_acf(df_train["y"], lags=20, ax=ax1)
fig = plt.figure(figsize=(20,8))
ax1 = fig.add_subplot(212)
fig = sm.graphics.tsa.plot_pacf(df_train["y"], lags=20, ax=ax1)
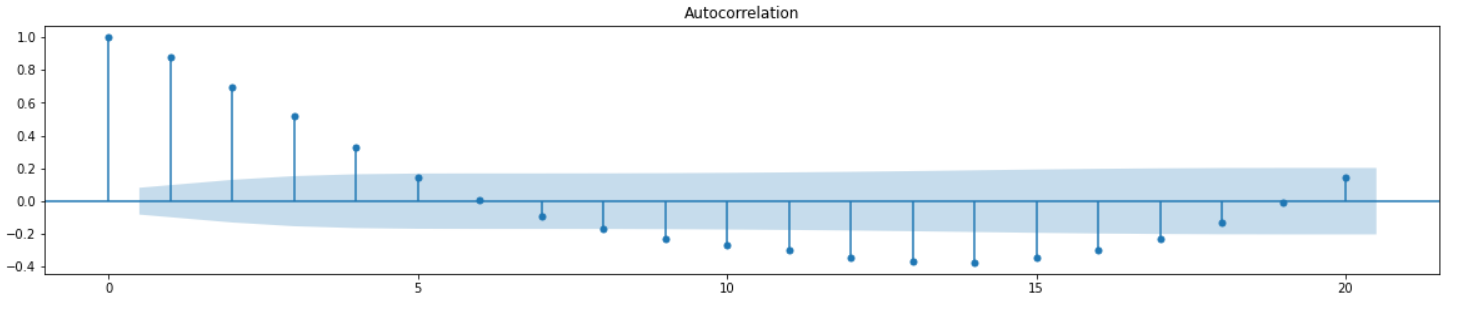
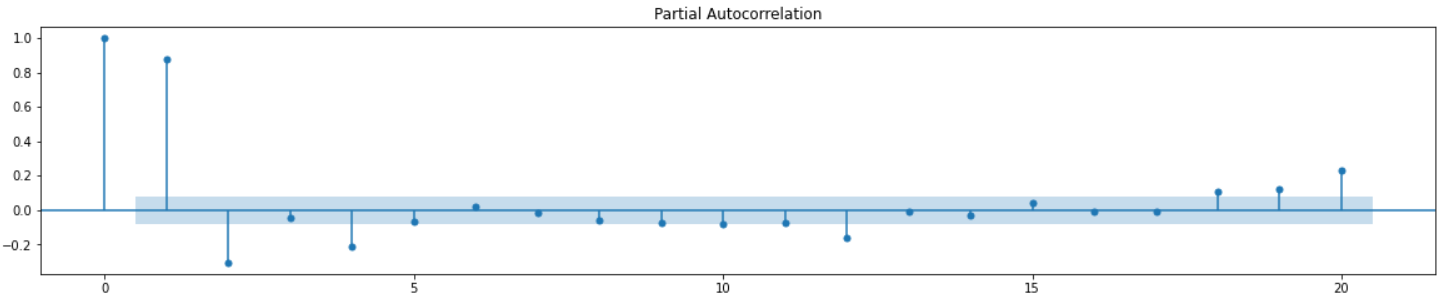
그래프의 확인해 보면 q=5, p=1인 것을 알 수 있다.
Modeling, Training, Evaluate
먼저 ARIMA를 이용하여 최적의 모델을 학습시키고 예측을 진행했다. 또한 데이터가 주기성을 가지고 있는 것이 확인 되었으므로 주기성을 추가로 고려하는 모델인 SARIMAX를 이용해서도 학습을 진행했다.
from statsmodels.tsa.arima.model import ARIMA
from statsmodels.tsa.statespace.sarimax import SARIMAX
import itertools
from tqdm import tqdm
ARIMA
최적의 파라미터를 찾기 위해 위에서 구한 범위가 들어가도록 grid search를 진행했다.
p = range(0,3)
d = range(1,2)
q = range(0,6)
pdq = list(itertools.product(p,d,q))
aic = []
params = []
with tqdm(total = len(pdq)) as pg:
for i in pdq:
pg.update(1)
try:
model = SARIMAX(df_train["y"], order=(i))
model_fit = model.fit()
aic.append(round(model_fit.aic,2))
params.append((i))
except:
continue
100%|██████████| 18/18 [00:08<00:00, 2.13it/s]
18개의 파라미터들에 대한 탐색을 진행했다.
optimal = [(params[i],j) for i,j in enumerate(aic) if j == min(aic)]
model_opt = ARIMA(df_train["y"], order = optimal[0][0])
model_opt_fit = model_opt.fit()
model_opt_fit.summary()
| Dep. Variable: | y | No. Observations: | 576 |
| Model: | ARIMA(2, 1, 4) | Log Likelihood | -1926.684 |
| Date: | Fri, 30 Jul 2021 | AIC | 3867.368 |
| Time: | 13:43:14 | BIC | 3897.849 |
| Sample: | 0 | HQIC | 3879.256 |
| - 576 | |||
| Covariance Type: | opg |
탐색된 파라미터들 중 aic가 가장 낮은 모델을 최적의 모델로 선택하였다.
최적의 파라미터는 (2,1,4) 이고 모델 학습의 결과는 위와 같다.
model = ARIMA(df_train["y"], order=optimal[0][0])
model_fit = model.fit()
forecast = model_fit.forecast(steps=24*7)
plt.figure(figsize=(20,5))
plt.plot(range(400,744), df["y"].iloc[400:])
plt.plot(forecast)
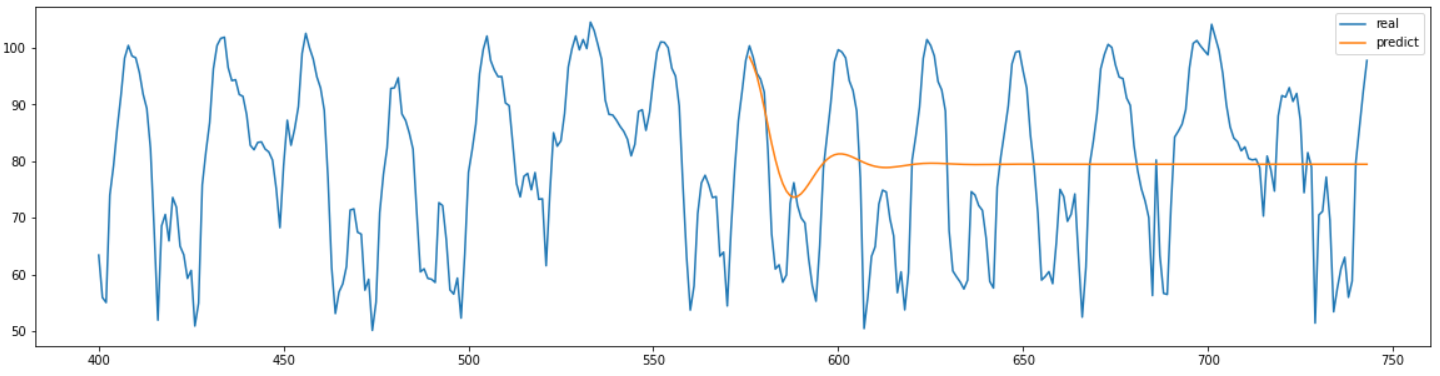
찾아낸 최적의 파라미터를 이용하여 모델을 학습시키고 결과를 실제 값과 동시에 그래프를 그려본 결과는 위와 같다.
결과를 확인해보면 처음 step들은 비슷하지만 바로 전혀 예측을 제대로 하지 못하는 것을 확인 할 수 있다.
SARIMAX: 24
ARIMA에서 데이터의 주기성을 추가로 고려해 주는 SARIMAX를 이용하여 학습을 진행했다.
파라미터의 탐색 범위는 이전과 동일하고, 주기에 대한 파라미터는 데이터가 24시간을 기준으로 반복되는 것을 확인했으므로 24로 설정하였다.
p = range(0,3)
d = range(1,2)
q = range(0,6)
m = 24
pdq = list(itertools.product(p,d,q))
seasonal_pdq = [(x[0],x[1], x[2], m) for x in list(itertools.product(p,d,q))]
aic = []
params = []
with tqdm(total = len(pdq) * len(seasonal_pdq)) as pg:
for i in pdq:
for j in seasonal_pdq:
pg.update(1)
try:
model = SARIMAX(df_train["y"], order=(i), season_order = (j))
model_fit = model.fit()
aic.append(round(model_fit.aic,2))
params.append((i,j))
except:
continue
100%|██████████| 324/324 [02:22<00:00, 2.27it/s]
324가지의 파라미터들에 대한 탐색을 진행하였다.
optimal = [(params[i],j) for i,j in enumerate(aic) if j == min(aic)]
model_opt = SARIMAX(df_train["y"], order = optimal[0][0][0], seasonal_order = optimal[0][0][1])
model_opt_fit = model_opt.fit()
model_opt_fit.summary()
| Dep. Variable: | y | No. Observations: | 576 |
| Model: | SARIMAX(2, 1, 4)x(0, 1, 0, 24) | Log Likelihood | -1919.823 |
| Date: | Fri, 30 Jul 2021 | AIC | 3853.646 |
| Time: | 10:24:02 | BIC | 3883.828 |
| Sample: | 0 | HQIC | 3865.440 |
| - 576 | |||
| Covariance Type: | opg |
가장 낮은 aic를 기준으로 찾은 최적의 모델의 결과는 위와 같다.
model = SARIMAX(df_train["y"], order=optimal[0][0][0], seasonal_order=optimal[0][0][1])
model_fit = model.fit(disp=0)
forecast = model_fit.forecast(steps=24*7)
plt.figure(figsize=(20,5))
plt.plot(range(400,744), df["y"].iloc[400:], label="real")
plt.plot(forecast, label="predict")
plt.legend()
plt.show()
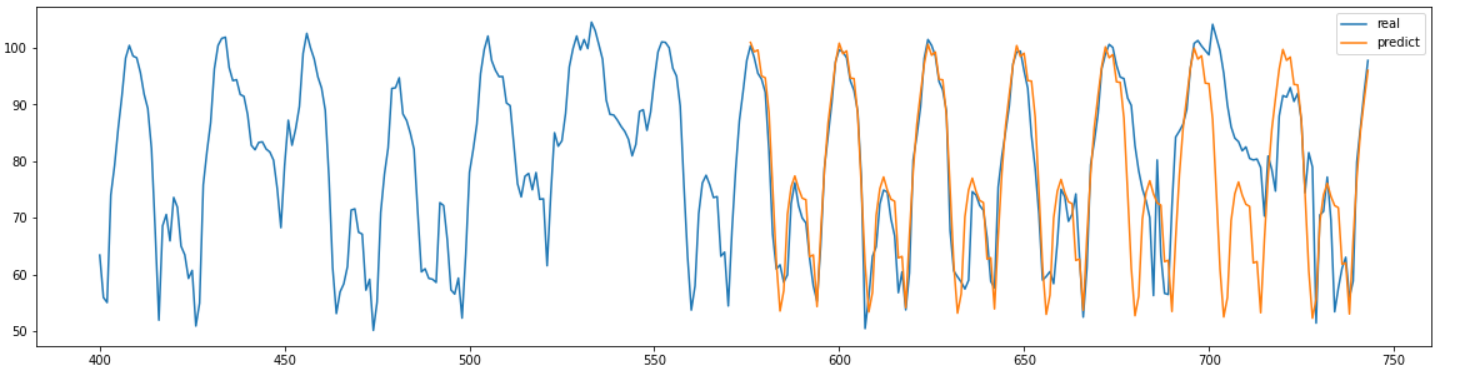
찾아낸 최적의 파라미터를 이용하여 모델을 학습시키고 결과를 실제 값과 동시에 그래프를 그려본 결과는 위와 같다.
이번에는 상당히 결과를 잘 예측한 것을 확인할 수 있다.
예측한 결과의 MAPE를 계산해 보았다.
def MAPEval(y_pred, y_true):
return np.mean(np.abs((y_true - y_pred) / y_true)) * 100
MAPEval(forecast, df["y"].iloc[-24*7:])
7.995463785651868
결과는 약 8.00으로 상당히 정확한 결과를 얻은 것을 알 수 있었다.
하지만 결과를 보면 일정한 주기의 데이터가 반복되는 형태여서 아래 그림과 요일마다 달라지는 부분은 예측을 하지 못하는 것을 확인했다.
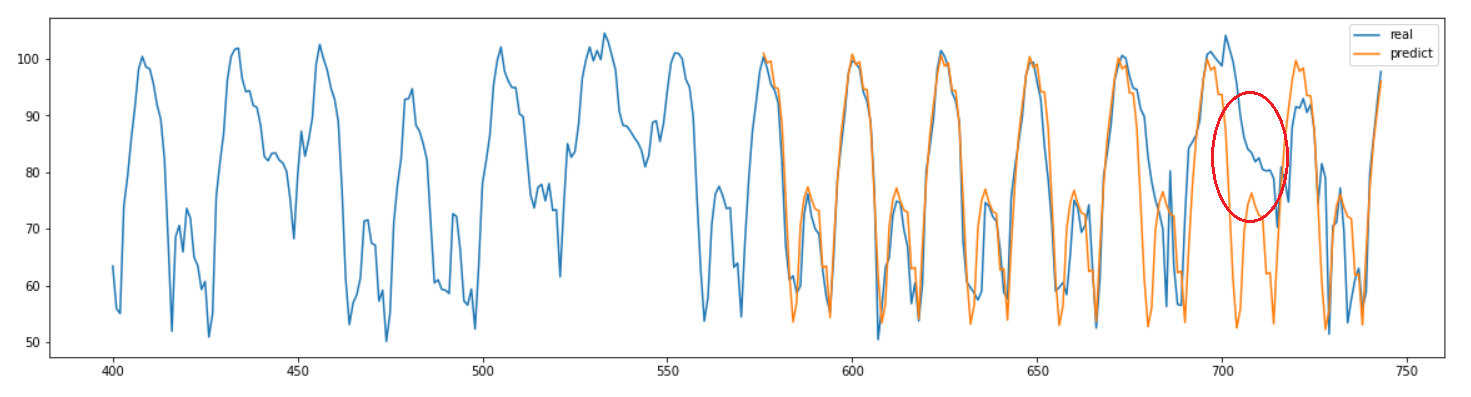
이러한 부분은 입력한 주기가 하루기 때문에 일주일 간격으로 나타나는 특성을 포착하지 못하는 것이라고 생각되었다.
이러한 부분을 개선하기 위해 주기를 일주일로 SARIMAX를 다시 진행해 보았다.
SARIMAX: 24*7
위의 모델에서 SARIMAX의 season_orderd의 마지막 값을 24*7로 변경하고 나머지 부분은 모두 동일하게 유지한 채 다시 학습을 진행해 보았다.
m = 27 => m= 27*7 #다른 과정은 이전과 동일
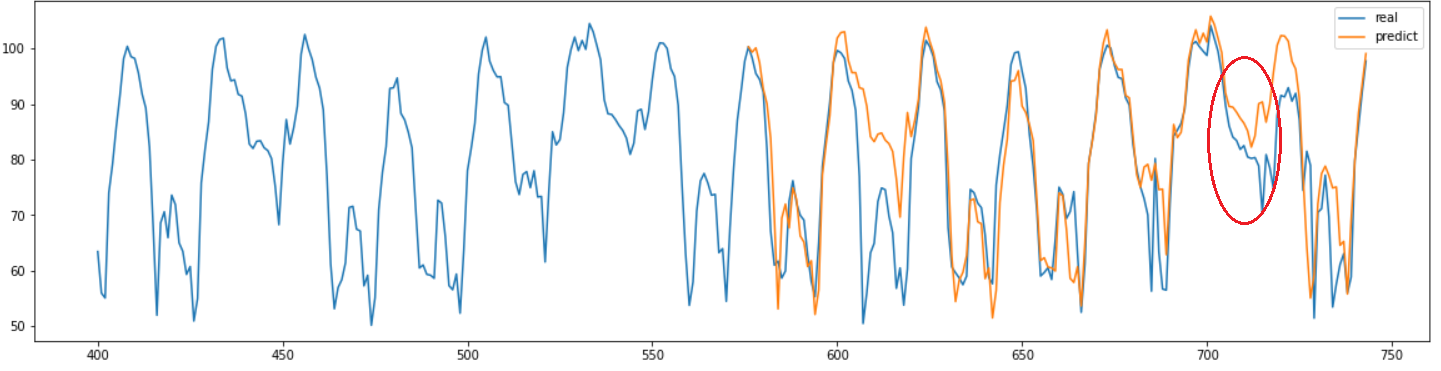
그 결과 이전에서는 포착하지 못했던 요일별 특성을 어느정도 포착한 것을 확인 할 수 있었다.
예측한 결과의 MAPE를 계산해 보았다.
def MAPEval(y_pred, y_true):
return np.mean(np.abs((y_true - y_pred) / y_true)) * 100
MAPEval(forecast, df["y"].iloc[-24*7:])
8.748684216744659
결과는 약 8.75으로 나쁘지 않지만 이전보다 성능이 더 떨어진 것을 확인 할 수 있었다.
Conclusion
ARIMA와 SARIMAX를 사용하여 평균속도를 예측해본 결과 ARIMA는 전혀 의미가 없는 결과가 나왔고, SARIMAX 의 하루 주기는 MAPE 8.00, 일주일 주기는 MAPE 8.75의 결과가 나온 것을 확인 할 수 있었다.
MAPE결과는 하루 주기가 더 좋은 결과가 나왔지만 MAPE 가 절대적인 지표가 아니므로 어떤 결과가 더 좋다고는 할 수 없을 것 같고 필요에 따라서 원하는 주기를 설정할 필요가 있어 보인다.
SARIMAX는 직접 입력한 주기의 값에 따라 결과가 많이 바뀐다는 것을 알 수 있었다.
SARIMAX는 데이터의 주기를 직접 입력해주어야 하고 입력한 주기에 영향을 많이 받기 때문에 주기를 모르는 상황이거나 주기가 일정하지 않은 데이터에서는 적용하기 힘들 것 같다는 생각이 들었다.
데이터의 주기를 알고 있고 주기가 일정하다면 빠르고 간편하게 적용해 볼 수 있는 방법인 것 같다.