[코드구현] Time Series Imputation - NAOMI (NeurIPS 2019)
한 시간 간격으로 측정 되어 있는 한 달치 특정 구간의 평균 속도 데이터를 이용하여 임의로 결측치를 만들고 결측치 대체해보는 task를 수행해 보았다.
데이터는 도로교통공사의 오픈 데이터를 직접 가공하였으며 아래에서 다운로드할 수 있다.
전에 번역했던 NAOMI: Non-AutOregressive Multiresolution sequence Imputation 논문을 코드로 구현하였으며 github의 official code를 참고했다.
paper: https://arxiv.org/pdf/1901.10946.pdf
code: https://github.com/felixykliu/NAOMI
NAOMI는 Divide & Conquer 방법을 사용하여 긴 길이의 결측치에서도 좋은 성능을 가질 수 있도록 한 모델이다. 논문의 자세한 내용은 아래에 있다.
Import Module
필요한 모듈들을 import 한다.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import MinMaxScaler
from torch.autograd import Variable
import torch
import torch.utils
import torch.utils.data
from torch import nn
from tqdm import trange
import sys
Load Data
데이터를 가져온다.
df = pd.read_csv("서인천IC-부평IC 평균속도.csv",encoding='CP949')
df2 = pd.DataFrame()
df2["time"] = pd.to_datetime(df["집계일시"],format="%Y%m%d%H%M")
df2["value"] = df["평균속도"]
missing_range = [(100,105),(200,210),(300,320),(400,430),(550,600)]
for start,end in missing_range:
df2.iloc[start:end,1] = np.nan
plt.figure(figsize=(20,5))
plt.plot(df2["value"])
plt.show()
df2.to_csv("data.csv", index=False)
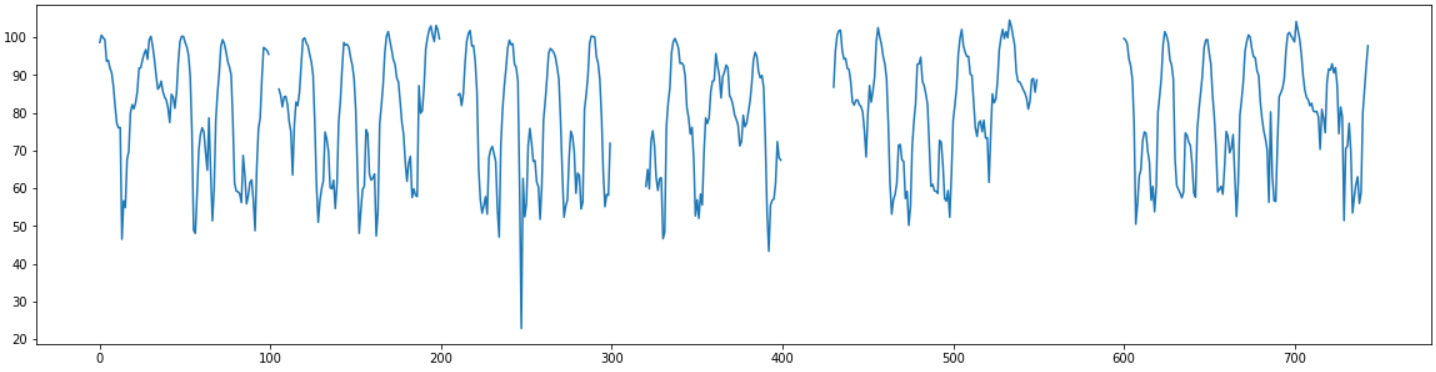
데이터는 한달치의 1시간 간격의 평균 속도 데이터로 총 744개의 데이터가 있다.
결측치는 5~50범위의 다양한 길이로 갈수록 결측범위가 길어지도록 임의의 구간에 직접 만들어 주었다.
def makeBatch():
df = pd.read_csv(path)
min_max_scaler = MinMaxScaler()
df = df[["time", "value"]]
df["value"] = min_max_scaler.fit_transform(df["value"].values.reshape(-1,1))
missing_list = df.isnull()["value"]
data = df["value"].to_numpy()
data_batch = []
datas = []
for index,val in enumerate(data):
if missing_list[index]:
datas=[]
continue
datas.append(val)
if len(datas)==window_size:
data_batch.append(datas.copy())
datas.pop(0)
data_batch = np.array(data_batch)
data_batch = data_batch.reshape(data_batch.shape[0], data_batch.shape[1], 1)
return df,data, min_max_scaler, data_batch
학습을 할 데이터를 만든다.
학습을 진행할 때는 결측치가 없는 데이터만 가지고 진행을 해야 한다.
실제 논문에서는 결측치가 없는 train_set이 따로 있었지만 여기서는 따로 train_set이 없기 때문에 정상정인 데이터만 있는 데이터셋을 따로 만들어주어야 했다.
window_size크기만큼 데이터를 잘라서 데이터 셋을 만들면서 그 안에는 결측치가 없도록 하기위해window_size만큼의 데이터를 한칸씩 sliding시키면서 데이터를 생성하면서, 결측치가 있을 경우 없을때까지 패스하는 방식으로 데이터를 생성했다.
Modeling
훈련을 진행할 NAOMI모델을 선언한다.
class NAOMI(nn.Module):
def __init__(self, params):
super(NAOMI, self).__init__()
self.params = params
self.task = params['task']
self.stochastic = (self.task == 'basketball')
self.y_dim = params['y_dim']
self.rnn_dim = params['rnn_dim']
self.dims = {}
self.n_layers = params['n_layers']
self.networks = {}
self.highest = params['highest']
self.batch_size = params['batch']
self.gru = nn.GRU(self.y_dim, self.rnn_dim, self.n_layers)
self.back_gru = nn.GRU(self.y_dim + 1, self.rnn_dim, self.n_layers)
step = 1
while step <= self.highest:
l = str(step)
self.dims[l] = params['dec' + l + '_dim']
dim = self.dims[l]
curr_level = {}
curr_level['dec'] = nn.Sequential(
nn.Linear(2 * self.rnn_dim, dim),
nn.ReLU())
curr_level['mean'] = nn.Linear(dim, self.y_dim)
if self.stochastic:
curr_level['std'] = nn.Sequential(
nn.Linear(dim, self.y_dim),
nn.Softplus())
curr_level = nn.ModuleDict(curr_level)
self.networks[l] = curr_level
step = step * 2
self.networks = nn.ModuleDict(self.networks)
def forward(self, data, ground_truth):
# data: seq_length * batch * 11
# ground_truth: seq_length * batch * 10
h = Variable(torch.zeros(self.n_layers, self.batch_size, self.rnn_dim))
h_back = Variable(torch.zeros(self.n_layers, self.batch_size, self.rnn_dim))
if self.params['cuda']:
h, h_back = h.cuda(), h_back.cuda()
loss = 0.0
h_back_dict = {}
count = 0
for t in range(data.shape[0] - 1, 0, -1):
h_back_dict[t+1] = h_back
state_t = data[t]
_, h_back = self.back_gru(state_t.unsqueeze(0), h_back)
for t in range(data.shape[0]):
state_t = ground_truth[t]
_, h = self.gru(state_t.unsqueeze(0), h)
count += 1
for l, dim in self.dims.items():
step_size = int(l)
curr_level = self.networks[str(step_size)]
if t + 2 * step_size <= data.shape[0]:
next_t = ground_truth[t+step_size]
h_back = h_back_dict[t+2*step_size]
dec_t = curr_level['dec'](torch.cat([h[-1], h_back[-1]], 1))
dec_mean_t = curr_level['mean'](dec_t)
if self.stochastic:
dec_std_t = curr_level['std'](dec_t)
loss += nll_gauss(dec_mean_t, dec_std_t, next_t)
else:
loss += torch.sum((dec_mean_t - next_t).pow(2))
return loss / count / data.shape[1]
def sample(self, data_list, batch_size = None):
if not batch_size:
batch_size = self.batch_size
# data_list: seq_length * (1 * batch * 11)
ret = []
seq_len = len(data_list)
h = Variable(torch.zeros(self.params['n_layers'], batch_size, self.rnn_dim))
if self.params['cuda']:
h = h.cuda()
h_back_dict = {}
h_back = Variable(torch.zeros(self.params['n_layers'], batch_size, self.rnn_dim))
if self.params['cuda']:
h_back = h_back.cuda()
for t in range(seq_len - 1, 0, -1):
h_back_dict[t+1] = h_back
state_t = data_list[t]
_, h_back = self.back_gru(state_t, h_back)
curr_p = 0
_, h = self.gru(data_list[curr_p][:, :, 1:], h)
while curr_p < seq_len - 1:
if data_list[curr_p + 1][0, 0, 0] == 1:
curr_p += 1
_, h = self.gru(data_list[curr_p][:, :, 1:], h)
else:
next_p = curr_p + 1
while next_p < seq_len and data_list[next_p][0, 0, 0] == 0:
next_p += 1
step_size = 1
while curr_p + 2 * step_size <= next_p and step_size <= self.highest:
step_size *= 2
step_size = step_size // 2
self.interpolate(data_list, curr_p, h, h_back_dict, step_size)
return torch.cat(data_list, dim=0)[:, :, 1:]
def interpolate(self, data_list, curr_p, h, h_back_dict, step_size):
#print("interpolating:", len(ret), step_size)
h_back = h_back_dict[curr_p + 2 * step_size]
curr_level = self.networks[str(step_size)]
dec_t = curr_level['dec'](torch.cat([h[-1], h_back[-1]], 1))
dec_mean_t = curr_level['mean'](dec_t)
if self.stochastic:
dec_std_t = curr_level['std'](dec_t)
state_t = reparam_sample_gauss(dec_mean_t, dec_std_t)
else:
state_t = dec_mean_t
added_state = state_t.unsqueeze(0)
has_value = Variable(torch.ones(added_state.shape[0], added_state.shape[1], 1))
if self.params['cuda']:
has_value = has_value.cuda()
added_state = torch.cat([has_value, added_state], 2)
if step_size > 1:
right = curr_p + step_size
left = curr_p + step_size // 2
h_back = h_back_dict[right+1]
_, h_back = self.back_gru(added_state, h_back)
h_back_dict[right] = h_back
zeros = Variable(torch.zeros(added_state.shape[0], added_state.shape[1], self.y_dim + 1))
if self.params['cuda']:
zeros = zeros.cuda()
for i in range(right-1, left-1, -1):
_, h_back = self.back_gru(zeros, h_back)
h_back_dict[i] = h_back
data_list[curr_p + step_size] = added_state
def num_trainable_params(model):
total = 0
for p in model.parameters():
count = 1
for s in p.size():
count *= s
total += count
return total
def nll_gauss(mean, std, x):
pi = Variable(torch.DoubleTensor([np.pi]))
if mean.is_cuda:
pi = pi.cuda()
nll_element = (x - mean).pow(2) / std.pow(2) + 2*torch.log(std) + torch.log(2*pi)
return 0.5 * torch.sum(nll_element)
def reparam_sample_gauss(mean, std):
eps = torch.DoubleTensor(std.size()).normal_()
eps = Variable(eps)
if mean.is_cuda:
eps = eps.cuda()
return eps.mul(std).add_(mean)
Train
선언한 모델을 가지고 학습을 진행한다.
def run_epoch(train, model, exp_data, clip, optimizer=None, batch_size=64, num_missing=None, teacher_forcing=True):
losses = []
inds = np.random.permutation(exp_data.shape[0])
i = 0
while i + batch_size <= exp_data.shape[0]:
ind = torch.from_numpy(inds[i:i+batch_size]).long()
i += batch_size
data = exp_data[ind]
data = data.to(device)
# change (batch, time, x) to (time, batch, x)
data = Variable(data.transpose(0, 1))
ground_truth = data.clone()
if num_missing is None:
#num_missing = np.random.randint(data.shape[0] * 18 // 20, data.shape[0])
num_missing = np.random.randint(data.shape[0] * 4 // 5, data.shape[0])
#num_missing = 40
missing_list = torch.from_numpy(np.random.choice(np.arange(1, data.shape[0]), num_missing, replace=False)).long()
data[missing_list] = 0.0
has_value = Variable(torch.ones(data.shape[0], data.shape[1], 1))
has_value = has_value.to(device)
has_value[missing_list] = 0.0
data = torch.cat([has_value, data], 2)
seq_len = data.shape[0]
if teacher_forcing:
batch_loss = model(data, ground_truth)
else:
data_list = []
for j in range(seq_len):
data_list.append(data[j:j+1])
samples = model.sample(data_list)
batch_loss = torch.mean((ground_truth - samples).pow(2))
if train:
optimizer.zero_grad()
total_loss = batch_loss
total_loss.backward()
nn.utils.clip_grad_norm_(model.parameters(), clip)
optimizer.step()
losses.append(batch_loss.data.cpu().numpy())
return np.mean(losses)
path = "data.csv"
window_size = 50
df, data, scaler, data_batch = makeBatch()
model = None
use_gpu = torch.cuda.is_available()
device = torch.device("cuda") if use_gpu else torch.device("cpu")
result = None
pretrain_epochs = 300
clip = 10
start_lr = 5e-3
batch_size = 64
np.random.seed(123)
torch.manual_seed(123)
if use_gpu:
torch.cuda.manual_seed_all(123)
params = {
'task' : "--",
'batch' : batch_size,
'y_dim' : 1,
'rnn_dim' : 50,
'dec1_dim' : 50,
'dec2_dim' : 50,
'dec4_dim' : 50,
'dec8_dim' : 50,
'dec16_dim' : 50,
'n_layers' : 2,
'discrim_rnn_dim' : 128,
'discrim_num_layers' : 2,
'cuda' : use_gpu,
'highest' : 8,
}
model = NAOMI(params).to(device)
params['total_params'] = num_trainable_params(model)
train_data = torch.Tensor(data_batch)
lr = start_lr
teacher_forcing = True
with trange(pretrain_epochs, file=sys.stdout) as tr:
for e in tr:
epoch = e+1
if epoch == pretrain_epochs // 2:
lr = lr / 2
optimizer = torch.optim.Adam(
filter(lambda p: p.requires_grad, model.parameters()),
lr=lr)
train_loss = run_epoch(True, model, train_data, clip, optimizer, batch_size = batch_size, teacher_forcing=teacher_forcing)
tr.set_postfix(loss="{0:.3f}".format(train_loss))
100%|██████████| 300/300 [04:40<00:00, 1.07it/s, loss=0.010]
Evaluate
학습된 모델을 이용하여 결과를 확인한다.
def predict_result():
test = data.copy()
missing_list = np.where(pd.isnull(test))
test[np.isnan(test)] = 0
test = test.reshape(len(data),1,1)
test = Variable(torch.Tensor(test).to(device))
has_value = Variable(torch.ones(test.shape[0], test.shape[1], 1))
has_value[missing_list] = 0.0
has_value = has_value.to(device)
data_test = torch.cat([has_value, test], 2)
data_list = []
for j in range(len(data)):
data_list.append(data_test[j:j+1])
samples = model.sample(data_list,1)
result = samples[:,0,0].cpu().detach().numpy()
result = scaler.inverse_transform(result.reshape(-1,1))
return result
result = predict_result()
df["value"] = result
data_ori = scaler.inverse_transform(data.reshape(-1,1))
plt.figure(figsize=(20,5))
plt.plot(data_ori, label="real", zorder=10)
plt.plot(result, label="predict")
plt.legend()
plt.show()
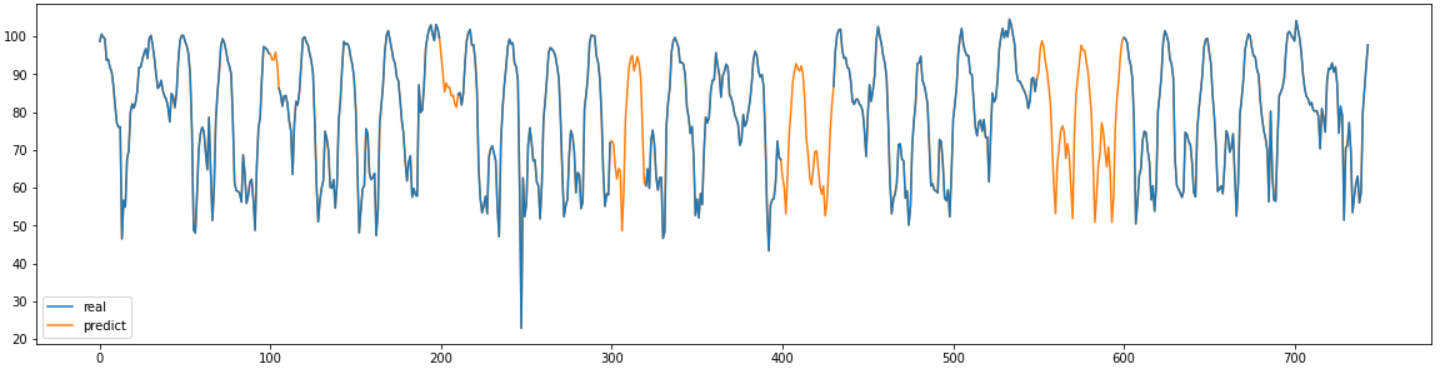
real = pd.read_csv("서인천IC-부평IC 평균속도.csv",encoding='CP949')
plt.figure(figsize=(20,5))
plt.plot(real["평균속도"], label="real")
lb = "predict"
for start, end in missing_range:
plt.plot(range(start-1,end+1), result[start-1:end+1], label=lb, color="orange")
lb=None
plt.legend()
plt.show()
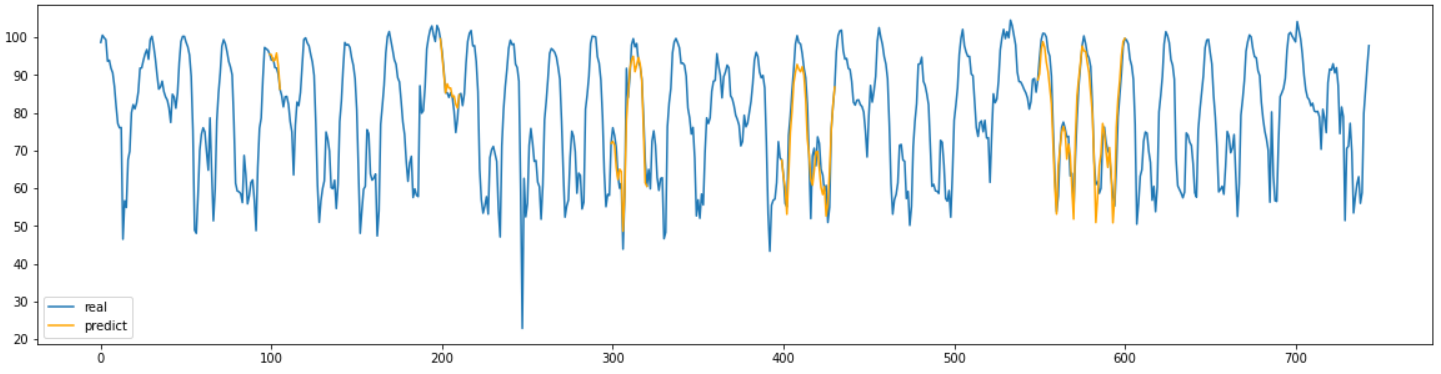
결과 그래프를 확인해 보면 결측치의 길이에 상관없이 대부분 잘 결측치를 대체한 것을 확인할 수 있다.
def MAPEval(y_pred, y_true):
return np.mean(np.abs((y_true - y_pred) / y_true)) * 100
realval = real["평균속도"].values
for start,end in missing_range:
print("길이{}인 구간의 MAPE:{:.3f}".format(end-start, MAPEval(result[start:end,0], realval[start:end])))
길이5인 구간의 MAPE:2.236
길이10인 구간의 MAPE:2.796
길이20인 구간의 MAPE:4.815
길이30인 구간의 MAPE:7.192
길이50인 구간의 MAPE:5.381
결측 구간의 MAPE를 계산해서 정확히 어느정도 수치로 정확한지 계산해 보았다.
MAPE값도 결측치의 길이에 상관없이 대부분 좋은 값을 가지고 있는 것을 확인했다.
Conclusion
시계열 데이터의 결측치 대체 모델인 NAOMI를 코드 구현하고 결과를 확인해 보았다.
긴 길이의 결측 구간도 잘 대체하기 위한 모델이라서 그런지 결측구간이 길어도 좋은 성능을 가지고 있는 것을 확인했다.
논문에서는 GAN을 사용해서 성능을 더욱 좋게 만들었다고 되어 있지만 실제로 GAN을 적용했을 때는 돌릴수록 더 성능이 나빠지기만 했다. GAN을 적용하기 전의 결과도 충분히 좋았기 때문에 GAN은 그냥 적용하지 않는 것으로 결정했다. GAN은 언제나 쉽지 않은 것 같다.
학습 방법의 특성상 학습 데이터를 만들 때 충분한 길이의 연속적인 정상데이터가 필요하다는 특징을 가지고있다.
연속적인 정상 데이터만 충분하다면 매우 좋은 성능을 보이는 결측치 대체 방법이라고 생각된다.