[코드구현] Time Series Forecasting - Transformer

Time Series Forecasting 프로젝트

 

한 시간 간격으로 측정 되어 있는 한 달치 특정 구간의 평균 속도 데이터를 이용하여 마지막 일주일 간의 평균 속도를 예측하는 task를 수행해 보았다.

Code

 

데이터는 도로교통공사의 오픈 데이터를 직접 가공하였으며 아래에서 다운로드할 수 있다.

csvfile

 

예전에 자연어 처리에서 자주 사용됐던 모델인 encoder decoder rnn (seq2seq) 모델은 시계열 예측에서도 좋은 성능을 보인다.

현재 자연어 처리에서 매우 뛰어난 성능을 보이는 Transformer가 시계열 예측에서도 좋은 성능을 보이는지 확인해 보기 위해 Transformer 모델을 이용하여 시계열 예측을 진행해 보았다.

Transformer 모델을 시계열 예측에 사용한 예시는 많이 없어서 내 생각대로 모델을 만들어서 예측을 진행했다.

 

Load Data

import numpy as np 
import pandas as pd 
import matplotlib.pyplot as plt

rawdata = pd.read_csv("서인천IC-부평IC 평균속도.csv", encoding='CP949')
plt.figure(figsize=(20,5))
plt.plot(range(len(rawdata)), rawdata["평균속도"])
rawdata.head()

	집계일시	평균속도
0	2021050100	98.63
1	2021050101	100.53
2	2021050102	99.86
3	2021050103	99.34
4	2021050104	93.64

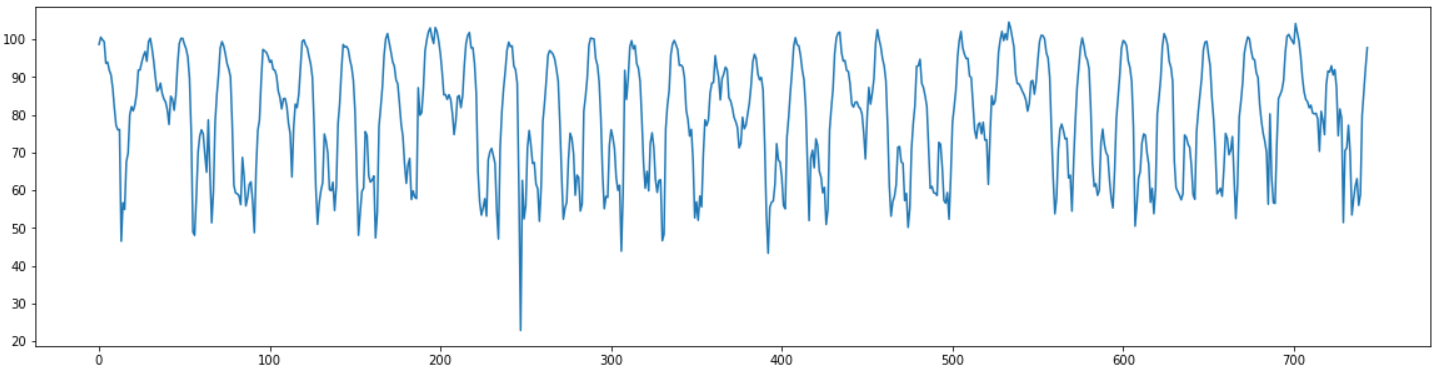
데이터를 보면 년, 월, 일, 시 가 있는 column과 평균속도의 값이 있는 column이 포함되어 있는 744개의 데이터가 있는 것을 확인 할 수 있다.

 

from sklearn.preprocessing import MinMaxScaler
min_max_scaler = MinMaxScaler()
rawdata["평균속도"] = min_max_scaler.fit_transform(rawdata["평균속도"].to_numpy().reshape(-1,1))

train = rawdata[:-24*7]
data_train = train["평균속도"].to_numpy()

test = rawdata[-24*7:]
data_test = test["평균속도"].to_numpy()

sklearn의 MinMaxSclaer를 사용하여 데이터의 범위를 0~1로 변환시켜준 후 마지막 일주일을 기준으로 train, test set을 나눠주었다.

 

Transformer Encoder, Transformer Decoder

transformer에 사용할 수 있도록 데이터 셋을 생성하고, torch의 nn.transformer를 사용해서 모델링을 진행했다.

 

Sliding Window Dataset

학습을 위해서는 인풋데이터와 아웃풋 데이터가 필요하다.

시계열 예측을 위해 데이터의 일정한 길이의 input window, output window를 설정하고, 데이터의 처음 부분부터 끝부분까지 sliding 시켜서 데이터셋을 생성했다.

input window를 모델의 인풋으로, output window를 모델의 아웃풋으로 사용한다.

 

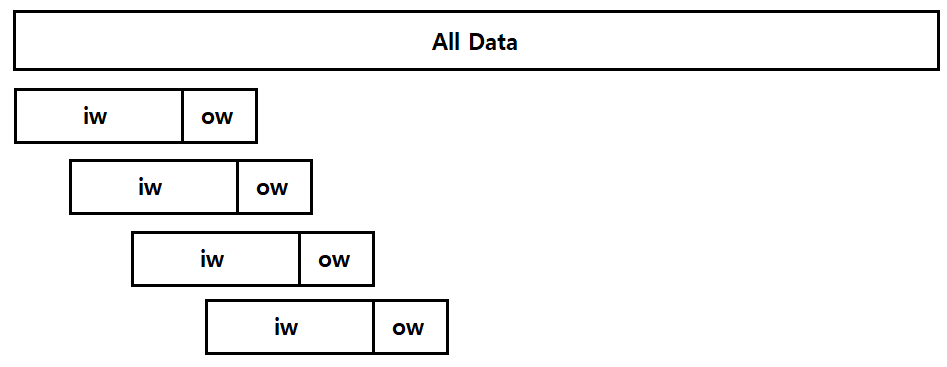
torch의 Dataset 클래스를 사용하여 window dataset을 생성하는 클래스를 선언했다.

from torch.utils.data import DataLoader, Dataset

class windowDataset(Dataset):
    def __init__(self, y, input_window=80, output_window=20, stride=5):
        #총 데이터의 개수
        L = y.shape[0]
        #stride씩 움직일 때 생기는 총 sample의 개수
        num_samples = (L - input_window - output_window) // stride + 1

        #input과 output
        X = np.zeros([input_window, num_samples])
        Y = np.zeros([output_window, num_samples])

        for i in np.arange(num_samples):
            start_x = stride*i
            end_x = start_x + input_window
            X[:,i] = y[start_x:end_x]

            start_y = stride*i + input_window
            end_y = start_y + output_window
            Y[:,i] = y[start_y:end_y]

        X = X.reshape(X.shape[0], X.shape[1], 1).transpose((1,0,2))
        Y = Y.reshape(Y.shape[0], Y.shape[1], 1).transpose((1,0,2))
        self.x = X
        self.y = Y
        
        self.len = len(X)
    def __getitem__(self, i):
        return self.x[i], self.y[i, :-1], self.y[i,1:]
    def __len__(self):
        return self.len

input window, output window, stride를 입력받고 iw+ow만큼의 길이를 stride간격으로 sliding하면서 데이터셋을 생성한다.

transformer의 input, decoder intput, output으로 활용하기 위해 세 가지의 값을 return하도록 만들었다.

첫 번째 값으로는 input window, 두 번째 값으로는 output window에서 마지막 값을 제외한 값, 마지막 값으로는 output window에서 첫 번째 값을 제외한 값을 return하도록 했다.

 

iw = 24*14
ow = 24*7

train_dataset = windowDataset(data_train, input_window=iw, output_window=ow, stride=1)
train_loader = DataLoader(train_dataset, batch_size=64)

output window의 크기로는 예측을 하려는 길이인 24*7로 설정했고, input window의 크기는 그 두배로 설정했다.

 

Modeling

이전에 챗봇을 제작할 때 사용했던 모델과 비슷하게 모델링을 진행했다. 그 때와 다른점은 인풋의 크기와 최종 아웃풋의 크기가 임베딩의 사이즈와 vocab size였던게 모두 1이 된 것이 다르다.

from torch.nn import Transformer
from torch import nn
import torch
import math

class TFModel(nn.Module):
    def __init__(self,d_model, nhead, nhid, nlayers, dropout=0.5):
        super(TFModel, self).__init__()
        self.transformer = Transformer(d_model=d_model, nhead=nhead, dim_feedforward=nhid, num_encoder_layers=nlayers, num_decoder_layers=nlayers,dropout=dropout)
        self.pos_encoder = PositionalEncoding(d_model, dropout)
        self.pos_encoder_d = PositionalEncoding(d_model, dropout)
        self.linear = nn.Linear(d_model, 1)
        self.encoder = nn.Linear(1, d_model)
        self.encoder_d = nn.Linear(1, d_model)

    def generate_square_subsequent_mask(self, sz):
        mask = (torch.triu(torch.ones(sz, sz)) == 1).transpose(0, 1)
        mask = mask.float().masked_fill(mask == 0, float('-inf')).masked_fill(mask == 1, float(0.0))
        return mask

    def forward(self, src, tgt, srcmask, tgtmask):
        src = self.encoder(src)
        src = self.pos_encoder(src)

        tgt = self.encoder_d(tgt)
        tgt = self.pos_encoder_d(tgt)
        output = self.transformer(src.transpose(0,1), tgt.transpose(0,1), srcmask, tgtmask)
        output = self.linear(output)
        return output

class PositionalEncoding(nn.Module):
    def __init__(self, d_model, dropout=0.1, max_len=5000):
        super(PositionalEncoding, self).__init__()
        self.dropout = nn.Dropout(p=dropout)

        pe = torch.zeros(max_len, d_model)
        position = torch.arange(0, max_len, dtype=torch.float).unsqueeze(1)
        div_term = torch.exp(torch.arange(0, d_model, 2).float() * (-math.log(10000.0) / d_model))
        pe[:, 0::2] = torch.sin(position * div_term)
        pe[:, 1::2] = torch.cos(position * div_term)
        pe = pe.unsqueeze(0).transpose(0, 1)
        self.register_buffer('pe', pe)

    def forward(self, x):
        x = x + self.pe[:x.size(0), :]
        return self.dropout(x)

def gen_attention_mask(x):
    mask = torch.eq(x, 0)
    return mask

데이터가 univariate time series이므로 input과 output의 차원은 모두 1차원이다.

인풋 데이터인 1차원의 벡터를 d_model의 차원으로 linear layer를 통해 바꿔준 후 positional encoding을 거쳐서 transformer를 통과하게 만들었다. 결과의 차원을 다시 1차원으로 만들어서 최종 output이 나오도록 했다.

자연어 처리때와는 달리 패딩없이 모든 데이터가 값을 가지고 있으므로 padding mask는 생략했다.

 

Training

device = torch.device("cuda")

lr = 1e-3
model = TFModel(256, 8, 256, 2, 0.1).to(device)
criterion = nn.MSELoss()
optimizer = torch.optim.Adam(model.parameters(), lr=lr)

epoch = 2000
from tqdm import tqdm

model.train()
progress = tqdm(range(epoch))
for i in progress:
    batchloss = 0.0
    
    for (inputs, dec_inputs, outputs) in train_loader:
        optimizer.zero_grad()
        src_mask = model.generate_square_subsequent_mask(inputs.shape[1]).to(device)
        tgt_mask = model.generate_square_subsequent_mask(dec_inputs.shape[1]).to(device)

        result = model(inputs.float().to(device), dec_inputs.float().to(device), src_mask, tgt_mask)
        loss = criterion(result.permute(1,0,2), outputs.float().to(device))
        
        loss.backward()
        optimizer.step()
        batchloss += loss
    progress.set_description("{:0.5f}".format(batchloss.cpu().item() / len(train_loader)))

0.00417: 100%|██████████| 2000/2000 [04:11<00:00,  7.97it/s]

만든 모델을 이용해서 학습을 진행했다.

MSELoss function을 사용했고, 2000번의 epoch로 학습을 진행했다.

 

Evaluate

학습된 모델을 이용해서 실제로 마지막 일주일의 데이터를 예측해 보았다.

def evaluate(length):
    input = torch.tensor(data_train[-24*7*2:]).reshape(1,-1,1).to(device).float().to(device)
    output = torch.tensor(data_train[-1].reshape(1,-1,1)).float().to(device)
    model.eval()
    for i in range(length):
        src_mask = model.generate_square_subsequent_mask(input.shape[1]).to(device)
        tgt_mask = model.generate_square_subsequent_mask(output.shape[1]).to(device)

        predictions = model(input, output, src_mask, tgt_mask).transpose(0,1)
        predictions = predictions[:, -1:, :]
        output = torch.cat([output, predictions.to(device)], axis=1)
    return torch.squeeze(output, axis=0).detach().cpu().numpy()[1:]

인풋 데이터로 train data의 마지막 2주일의 데이터를 사용하고, 디코더의 인풋으로는 train data의 마지막 값을 사용했다.

다음 값을 예측하는 과정을 예측할 길이만큼 반복하면서 output을 update했다.

원하는 길이 만큼 예측을 완료하면 최종값을 return한다.

 

result = evaluate(24*7)
result = min_max_scaler.inverse_transform(result)
real = rawdata["평균속도"].to_numpy()
real = min_max_scaler.inverse_transform(real.reshape(-1,1))

plt.figure(figsize=(20,5))
plt.plot(range(400,744),real[400:], label="real")
plt.plot(range(744-24*7,744),result, label="predict")
plt.legend()
plt.show()

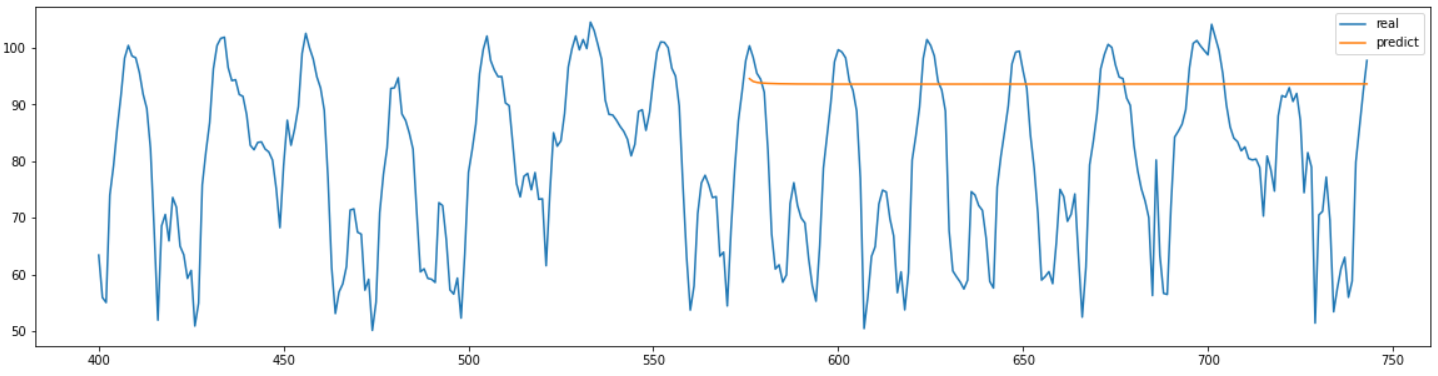
최종적으로 예측한 결과는 위 그림과 같다.

결과를 보면 의미있는 값을 전혀 예측하지 못한 것을 확인할 수 있다.

여러 하이퍼 파라미터를 바꿔보면서 학습을 진행해 봐도 비슷한 결과가 나왔으며, 전혀 예측을 하지 못했다.

24*7이라는 많은 step의 예측을 반복적으로 디코더에서 한개의 값씩 결과를 예측할 만큼 충분한 정보를 학습하지 못하는 것이라고 생각된다.

 

결과를 개선하기 위해 decoder에서 결과를 반복적으로 1step씩 예측하는게 아니라 FC layer를 통해 한번에 예측하는 모델로 다시 모델링을 진행해 보았다.

 

Transformer Encoder, FC layer Decoder

예측해야할 step의 개수가 많기 때문에 1step씩 결과를 예측을 하는 모델로는 좋은 결과를 얻어내지 못했다.

따라서 인코더의 아웃풋에서 FC layer를 통해 모든 결과를 한번에 예측하는 모델로 다시 시계열 예측을 시도해 보았다.

 

Dataset

이전과 거의 동일하지만 return하는 값이 input, output 두개 뿐이라는 점이 다르다.

from torch.utils.data import DataLoader, Dataset
class windowDataset(Dataset):
    def __init__(self, y, input_window=80, output_window=20, stride=5):
        #총 데이터의 개수
        L = y.shape[0]
        #stride씩 움직일 때 생기는 총 sample의 개수
        num_samples = (L - input_window - output_window) // stride + 1

        #input과 output
        X = np.zeros([input_window, num_samples])
        Y = np.zeros([output_window, num_samples])

        for i in np.arange(num_samples):
            start_x = stride*i
            end_x = start_x + input_window
            X[:,i] = y[start_x:end_x]

            start_y = stride*i + input_window
            end_y = start_y + output_window
            Y[:,i] = y[start_y:end_y]

        X = X.reshape(X.shape[0], X.shape[1], 1).transpose((1,0,2))
        Y = Y.reshape(Y.shape[0], Y.shape[1], 1).transpose((1,0,2))
        self.x = X
        self.y = Y
        
        self.len = len(X)
    def __getitem__(self, i):
        return self.x[i], self.y[i]
    def __len__(self):
        return self.len

iw = 24*14
ow = 24*7

train_dataset = windowDataset(data_train, input_window=iw, output_window=ow, stride=1)
train_loader = DataLoader(train_dataset, batch_size=64)

첫번째 값에서는 input window크기의 input data, 두번째 값에서는 output window 크기의 output data를 return한다.

 

Modeling

transformer decoder를 사용하지 않고 transformer encoder의 output에 FC Layer를 연결해서 결과를 바로 예측한다.

class TFModel(nn.Module):
    def __init__(self,iw, ow, d_model, nhead, nlayers, dropout=0.5):
        super(TFModel, self).__init__()
        self.encoder_layer = nn.TransformerEncoderLayer(d_model=d_model, nhead=nhead, dropout=dropout)
        self.transformer_encoder = nn.TransformerEncoder(self.encoder_layer, num_layers=nlayers) 
        self.pos_encoder = PositionalEncoding(d_model, dropout)

        self.encoder = nn.Sequential(
            nn.Linear(1, d_model//2),
            nn.ReLU(),
            nn.Linear(d_model//2, d_model)
        )
        
        self.linear =  nn.Sequential(
            nn.Linear(d_model, d_model//2),
            nn.ReLU(),
            nn.Linear(d_model//2, 1)
        )

        self.linear2 = nn.Sequential(
            nn.Linear(iw, (iw+ow)//2),
            nn.ReLU(),
            nn.Linear((iw+ow)//2, ow)
        ) 

    def generate_square_subsequent_mask(self, sz):
        mask = (torch.triu(torch.ones(sz, sz)) == 1).transpose(0, 1)
        mask = mask.float().masked_fill(mask == 0, float('-inf')).masked_fill(mask == 1, float(0.0))
        return mask

    def forward(self, src, srcmask):
        src = self.encoder(src)
        src = self.pos_encoder(src)
        output = self.transformer_encoder(src.transpose(0,1), srcmask).transpose(0,1)
        output = self.linear(output)[:,:,0]
        output = self.linear2(output)
        return output

class PositionalEncoding(nn.Module):
    def __init__(self, d_model, dropout=0.1, max_len=5000):
        super(PositionalEncoding, self).__init__()
        self.dropout = nn.Dropout(p=dropout)

        pe = torch.zeros(max_len, d_model)
        position = torch.arange(0, max_len, dtype=torch.float).unsqueeze(1)
        div_term = torch.exp(torch.arange(0, d_model, 2).float() * (-math.log(10000.0) / d_model))
        pe[:, 0::2] = torch.sin(position * div_term)
        pe[:, 1::2] = torch.cos(position * div_term)
        pe = pe.unsqueeze(0).transpose(0, 1)
        self.register_buffer('pe', pe)

    def forward(self, x):
        x = x + self.pe[:x.size(0), :]
        return self.dropout(x)

def gen_attention_mask(x):
    mask = torch.eq(x, 0)
    return mask

다음과 같은 순서로 진행되도록 모델링 했다.

• 1차원 벡터를 d_model 차원으로 바꿔준다.
  (batch, input_window, 1) => (batch, input_window, d_model)

• transformer encoder를 통과한다.
  (batch, input_window, d_model) => (batch, input_window, d_model)
• 결과의 d_model차원을 1차원으로 바꿔준다.
  (batch, input_window, d_model) => (batch, input_window, 1)
• 1차원인 부분을 없앤다.
  (batch, input_window, 1) => (batch, input_window)
• input_window차원을 output_window차원으로 바꿔준다.
  (batch, input_window) => (batch, output_window)

input window의 attention의 조합으로 output window를 바로 예측할 수 있다는 가정으로 모델을 만들었다.

linear layer들은 두 개씩 쌓아줬다.

 

Training

선언한 모델로 학습을 진행한다.

device = torch.device("cuda")
lr = 1e-4
model = TFModel(24*7*2, 24*7, 512, 8, 4, 0.1).to(device)
criterion = nn.MSELoss()
optimizer = torch.optim.Adam(model.parameters(), lr=lr)

epoch = 1000
model.train()
progress = tqdm(range(epoch))
for i in progress:
    batchloss = 0.0
    for (inputs, outputs) in train_loader:
        optimizer.zero_grad()
        src_mask = model.generate_square_subsequent_mask(inputs.shape[1]).to(device)
        result = model(inputs.float().to(device),  src_mask)
        loss = criterion(result, outputs[:,:,0].float().to(device))
        loss.backward()
        optimizer.step()
        batchloss += loss
    progress.set_description("loss: {:0.6f}".format(batchloss.cpu().item() / len(train_loader)))

loss: 0.002308: 100%|██████████| 1000/1000 [04:58<00:00,  3.35it/s]

MSELoss 로 1000번의 epoch로 학습을 진행했다.

 

Evaluate

학습된 모델을 이용해서 실제로 마지막 일주일의 데이터를 예측해 보았다.

def evaluate():
    input = torch.tensor(data_train[-24*7*2:]).reshape(1,-1,1).to(device).float().to(device)
    model.eval()
    
    src_mask = model.generate_square_subsequent_mask(input.shape[1]).to(device)
    predictions = model(input, src_mask)
    return predictions.detach().cpu().numpy()

train data의 마지막 2주일의 데이터를 input으로 사용해서 그 후 일주일의 데이터를 예측하는 함수를 만들었다.

 

result = evaluate()
result = min_max_scaler.inverse_transform(result)[0]
real = rawdata["평균속도"].to_numpy()
real = min_max_scaler.inverse_transform(real.reshape(-1,1))[:,0]


plt.figure(figsize=(20,5))
plt.plot(range(400,744),real[400:], label="real")
plt.plot(range(744-24*7,744),result, label="predict")
plt.legend()
plt.show()

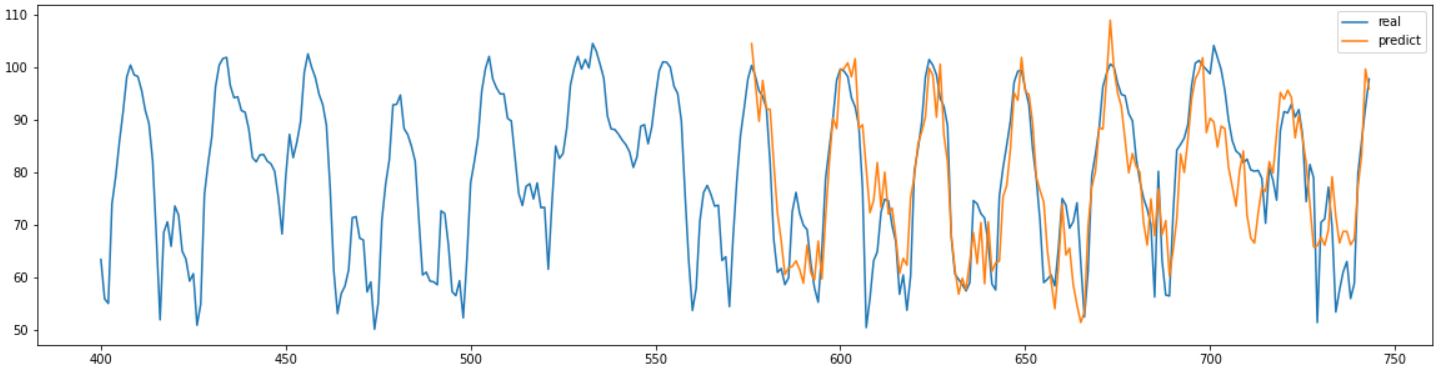
예측한 결과는 위 그래프와 같다.

결과를 보면 아까와는 달리 어느정도 결과를 잘 예측한 것을 확인할 수 있다.

 

def MAPEval(y_pred, y_true):
    return np.mean(np.abs((y_true - y_pred) / y_true)) * 100

MAPEval(result, real[-24*7:])

8.396453852281164

결과의 MAPE를 계산해본 결과 약 8.40으로 좋은 수치를 가지고 있는 것을 확인했다.

 

Conclusion

최근에 자연어 처리에서 매우 뛰어난 성능을 보여주고 있는 Transformer를 이용해서 시계열 예측을 진행해본 결과 transformer decoder를 사용했을 때는 좋은 결과를 얻지 못했지만 FC layer decoder를 사용했을 때는 MAPE 8.40의 좋은 성능을 확인할 수 있었다.

자연어처리의 용도로만 사용했었던 모델이 시계열 예측에서도 좋은 성능을 보이는 것을 확인하니까 transformer 모델의 활용 가능성이 정말 무궁무진할 수 있다는 생각이 들었다.

input window, output window 외의 다른 입력이 필요하지 않으므로 아무 데이터에도 적용가능하기 때문에 활용성이 높다고 생각된다.

GPU memory사용량이 좀 크다는 점과, 학습시간이 길어서 하이퍼 파라미터 튜닝을 많이 못해본 점이 조금 아쉽지만 시계열 예측을 할 때 충분히 한번쯤 시도해볼만한 가치가 있을 만큼 나쁘지 않은 방법인것 같다.