[논문번역] BRITS: bidirectional recurrent imputation for time series (NeurIPS 2018)

paper: https://arxiv.org/pdf/1805.10572.pdf

code: https://github.com/caow13/BRITS

 

Abstract

어떠한 가정도 필요없이 missing values를 바로 imputation하는 모델

세가지 장점

1. 시계열 데이터에서 여러개의 결측치를 다룰 수 있다.
2. 비선형 동역학 기반으로 시계열을 일반화한다.
3. 데이터 기반의 imputation 과정을 제공하고, 결측 데이터가 있는 일반적인 상황에 적용가능하다.

 

우리의 모델을 다음과 같은 세가지의 실제 데이터셋에서 평가해보았다.

공기질 데이터, 헬스케어 데이터, 사람의 활동에 대한 지역화 데이터

그 결과 우리의 모델은 imputation과 classification/regression에서 최신 방법을 능가하는 성능을 보여줬다.

 

Introduction

다변수 시계열 데이터는 결측치가 흔하기 때문에 imputation은 매우 중요하다.

기존의 연구에서는 결측치를 통계 혹은 ml기반으로 고치는 방향으로 접근했다.

그러나 대부분의 그러한 연구들에서는 결측치에 대한 강한 가정이 필요하다. 예시로

전통적인 통계 기반의 ARMA, ARIMA는 선형이어야 하고, kreindler는 데이터가 smoothable하다고 가정했고, Matrix completion은 통계 자료에만 사용될 수 있고 low-rankness와 같은 강한 가정이 필요하다. 관측 기반의 데이터 생성 모델은 가상 모델의 분포를 따른다는 가정이 필요하다. 아무튼 가정이 다들 많이 필요하다.

이 논문에 우리는 다 변수의 시계열 데이터에서 결측치를 채울 수 있는 BRITS라는 새로운 방법을 제안했다. 내부적으로 BRITS는 결측치를 채우기 위해 RNN을 적용했고, 데이터에 대한 어떠한 특별한 가정도 필요없다.

우리는 다음과 같은 기술적 기여를 했다.

• 결측치를 채우기 위해 우리는 양방향 RNN모델을 디자인했다. 우리는 smoothing을 위해 weight를 튜닝하는거 대신(GRU-D), RNN을 바로 결측치 예측에 사용했다. 우리 방법은 특별한 가정을 하지 않기 때문에 이전 방법들보다 더 일반적으로 사용 가능하다.
• 우리는 결측치를 backpropagation 과정과 관련된 양방향 RNN그래프의 변수로 사용했다. 이러한 경우에 앞과 뒤 모든 방향에서 일정한 제약과 함께 지연된 gradients 가 발생되면서 결측값 추정을 더 정확하게 한다.
• 우리는 하나의 뉴럴 그래프에서 결측치 imputation과 classification/regression 작업을 동시에 진행했다. 이렇게 하면 에러 전파 문제가 imputation에서 classification/regression으로 완화된다. 추가로, classification/regression의 라벨이 결측치를 더욱 정확하게 예측하게 한다.
• 우리는 우리의 모델을 세가지의실제 데이터셋에서 평가해보았다. 실험 결과 우리의 모델은 imputation과 classification/regression 정확도에서 모두 state-of-the-art를 능가하는 성능을 가지고 있었다.

 

Preliminary

x,m,delta에 대해 설명

x는 데이터, m은 결측치인지 아닌지 여부, delta는 마지막 관측값에서의 시간

 

BRITS

먼저 같은 시간에 관측된 변수들끼리 서로 상관 관계가 없을 때

 

Unidirectional Uncorrelated Recurrent Imputation (RITS-I)

가장 단순한 경우, 우리는 t번째 time step에서 변수들이 상관관계가 없다고 가정할 수 있다.

우리는 먼저 이러한 경우에 사용하는 RITS-I라는 imputation 알고리즘을 제안한다.

unidirectional recurrent dynamical system 에서 각 시계열 변수는 고정된 임의의 함수에서 얻어올 수 있다. 그래서 우리는 시계열의 모든 변수를 반복적인 역학에 따라 반복적으로 채운다.

t번째 step에서 만약 x_t가 실제로 관측 됐다면, 우리는 그것을 우리의 imputation을 검증하기 위해 사용하고 다음 반복 step으로 x_t를 전달한다. 그렇지 않다면 미래의 관측이 현재의 값과 관련되어 있기 때문에 x_t를 얻은 대체 값으로 대체하고, 미래의 관측값으로 검증한다.

 

x1~x10까지의 값들 중 x5,x6,x7이 missing일 때의 예시이다.

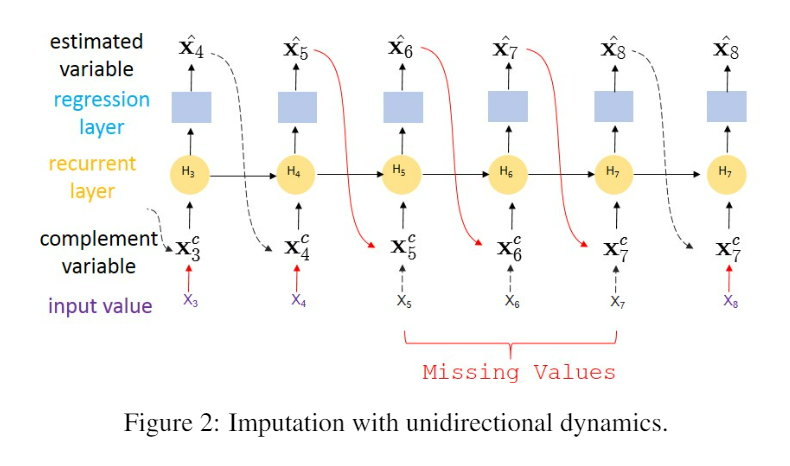
각각의 time step에서 한칸 t-1 step의 값을 이용해서 t step의 값을 추정할 수 있다.

처음 4번째 step 까지는 estimation error는 loss function (loss(x,x’))을 이용해서 즉시 구할 수 있다.

하지만 t가 5,6,7이면 실제 값이 없기 때문에 error를 즉시 계산할 수 없다.

하지만 8번째 step에서 x8^hat(추정값)은 x₅^{^} ~ x₇^{^}에 의존한다.

그래서 8번째 step에서는 5,6,7의 지연된 에러를 얻는다.

  

algorithm

우리는 imputation을 위해 recurrent component와 regression component를 소개한다.

recurrent component는 RNN에서 얻을 수 있고, regression component는 FC network에서 얻을 수 있다.

 

평범한 RNN은 다음과 같이 표현된다.

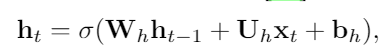
W,U,b는 파라미터, x는 input, h는 이전 단계의 hidden state이다.

 

우리의 경우, x_t가 결측값이라고 하면 x_t의 값을 위의 식처럼 바로 사용할 수 없다.

우리는 x_t가 결측값일 때 우리의 알고리즘에 의해 구해지는 complement input 인 x_t^c를 대신 사용했다.

 

공식적으로, 우리는 처음의 hidden state h₀를 all-zero vector로 초기화했고 아래와 같은 방법으로 모델을 업데이트 했다.

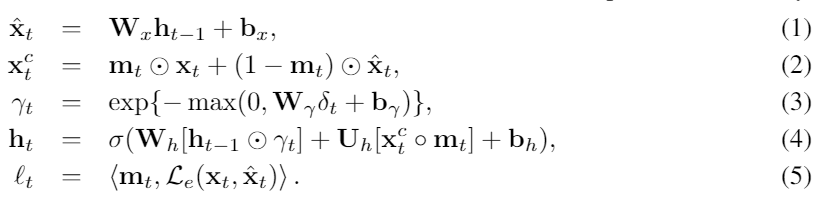
(1)은 hidden state h_t-1를 estimated vector 로 변환하는 regression component이다.

(2)에서는, 우리는 결측치를 (1)에서 구한 값을 이용하여 대체하고 대체값인 x_t^c를 얻어낸다.

그리고, 시계열 데이터는 아마 불규칙적으로 샘플링 되었기 때문에 (3)에서 우리는 hidden vector를 decay시키기 위해 temporal decay factor 감마를 추가로 사용한다.

(3)에서 만약 델타가 크다면 (오랜 기간동안 값이 missing인 경우) 작은 감마값이 나와서 hidden state를 많이 decay시킬 것을 알 수 있다.

이러한 요소는 imputation에 중요한 시계열에서 결측 패턴을 나타내는 것 또한 나타낸다.

(4)에서, decay된 hidden state에 기반하여, 우리는 다음 hidden stae를 예측한다.

(4)에있는 동그라미는 concatenate를 의미한다.

평균시간동안, 우리는 (5)와 같은 추정 손실함수를 이용하여 추전 오차를 계산했다.

우리의 실험에서, 우리는 Le함수로 mean absolute error를 사용했다. 최종적으로 우리는 작업 라벨 y를 다음과 같이 예측한다.

 

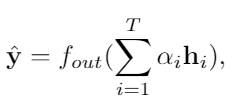
f_out는 특정한 작업에 의존하는 fc layer나 softmax layer가 될 수 있다. 알파는 hidden state마다 다른 attention 메커니즘이나 mean pooling 메커니즘에 의해 나오는 가중치 이다. (i.e. 알파 = 1/T)

우리는 아웃풋 로스를 L(y,y’)을 통해 구한다. 우리의 모델은 아래와 같은 로스를 최소화 시키면서 업데이트 된다.

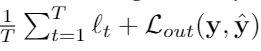
만약 classification 없이 순수하게 imputation만 하고 싶다면 앞에 있는거만 loss로 계산하면 된다.

 

 

Practical Issues

실제로는 vanilla RNN은 gradient vanishing 문제가 있기 때문에 우리는 LSTM을 (4)에서의 recurrent component로 사용한다. LSTM을 포함한 보통의 RNN 모델은 Xthat을 상수로 취급한다.

backpropagation동안 gradients는 xthat에서 잘리게 된다. 이것은 에러를 추정하는데에 backpropagation이 충분하지 않게 만든다.

예를 들어 아까 예시에서 xhat5,6,7에서의 추정 에러는 8번째 스텝에서 지연된 에러로 얻게 된다. 이렇게 되면 xhat5,6,7이 상수가 되고 지연된 에러는 완벽하게 backpropagate되지 못하게 된다.

(관측값이 결측치인 동안 x가 계속 같은 값을 가져서 backpropagation이 잘 안된다는 뜻)

이러한 문제를 해결하기 위해서 우리는 x를 RNN에서 변수로 사용한다. 우리는 backpropagation 중에 추정 에러가 x를 통과하도록 했다.

아까 예시에서, gradients가 실선의 반대 방향을 통해 backpropagated된다.

그래서 지연된 에러 l8이 5,6,7번 step을 통과한다.

이 실험에서 우리는 우리의 모델이 x를 상수로 사용했을때 불안정한 것을 찾았다.

지금까지 설명한게 RITS-I 다

 

Bidirectional Uncorrelated Recurrent Imputation (BRITS-I)

RITS-I에서 결측치의 추정된 에러는 다음 관측이 있을때 까지 지연된다.

이러한 에러 지연은 모델 수렴을 느리게하고 학습을 비효율적으로 한다. 평균적으로 bias exploding 문제를 일으키기도 한다.

여기에서는 우리는 BRITS-I라는 발전된 버전을 제안한다.

이 알고리즘은 bidirectional recurrent dynamics를 이용해서 위에서 언급한 이슈를 완화한다.

아까의 예시로 다시 설명하면 bidirectional recurrent dynamics에서는 x4가 반대로 x5~x7에 영향을 받는다. 따라서 5번째 step의 에러가 8번째 step의 forward direction뿐만 아니라 4번째 step의 backward direction에도 영향을 받게 된다.

그러면 sequence도 forward, backward두개가 생기고 그거에 따른 loss sequence 도 두개가 생긴다.

우리는 “consistency loss”를 도입하여 각 단계의 예측을 양방향으로 일관되게 시행한다.

우리는 mean squared error를 discrepancy 로 사용핸다.

최종적인 추정 loss는 forward loss, backward loss, consistency loss를 모두 합쳐서 얻는다.

t번째 step에서 최종 결과는 forward x와 backward x의 평균이다.

 

Correlated Recurrent Imputation (BRITS)

RITS-I와 BRITS-I에서 같은 시간에 관측된 특징끼리 모두 상관이 없다고 가정했다. 하지만 몇몇의 경우 이것은 사실이 아니다.

일반적으로 어떤 장치에서 측정된 값들은 그 근처에서 측정된 장치들과 비슷한 값을 가지고 있다. 이러한 경우에 우리는 그 둘의 과거의 데이터를 통해 결측값을 추정할 수 있다.

지금까지 고려한 것은 history-based estimation이었지만 여기에서는 이거와는 다른 다른 feature-based estimation을 얻어낸다.

t번째 step에서 우리는 complement observation x_t^c를 (1), (2)를 통해 얻고 난 후, 우리는 feature-based estimation 을 다음과 같이 정의한다.

W,b는 파라미터다

우리는 W의 대각 행렬을 모두 0으로 제한했다. 그래서 z의 d번째 element는 x_t^d의 추정치이다.

 

우리는 추가로 historical-based estimation x와 feature-based estimation z를 아래와 같은 방법으로 c로 합쳤다.

 

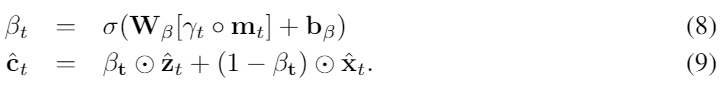
beta를 감마와 m을 고려하면서 학습하면 된다.

남은 부분은 앞의 brits-i때와 비슷하다. x의 결측치를 c로 대체하고 다음 h값을 얻는다.

 

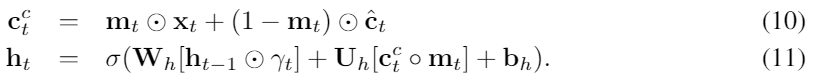
그러나 추정 loss는 feature uncorrelated 경우와 다르다. 우리는 단순히 L(x,c)를 사용하는 것이 모델이 수렴하는데에 매우 느리게 작용하는 것을 알았다.

그래서 우리는 모든 추정 에러들을 합쳐서 loss로 사용한다.

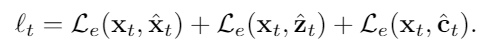
최종적인 로스

 

Test

오픈되어 있는 도로 교통 데이터에 자체적으로 데이터를 없애고 이 방법을 직접 적용해 본 결과는 아래와 같다.

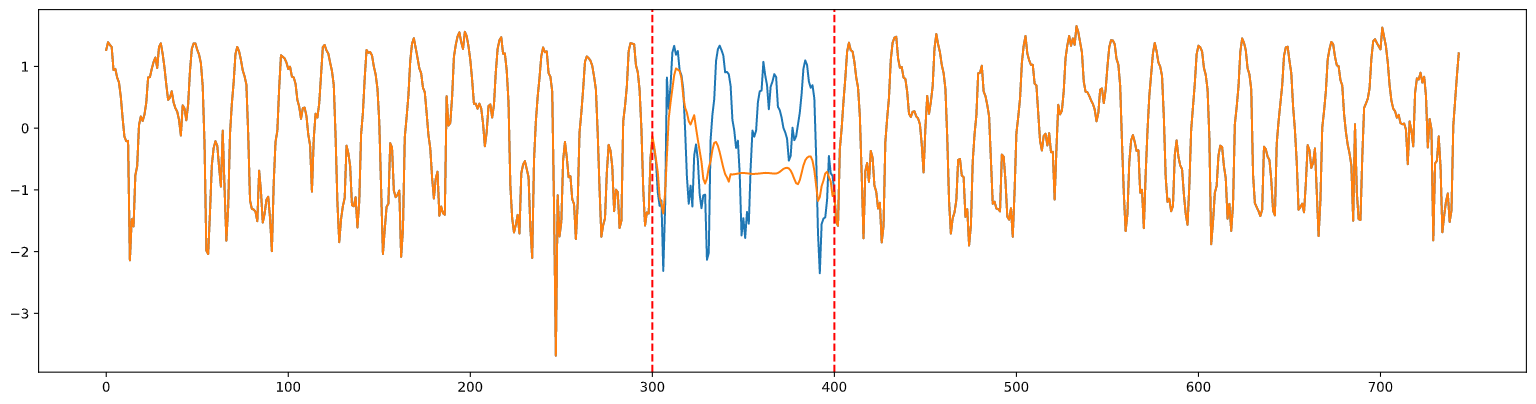
관측된 값이 나올 때 까지 상태를 저장하고 관측된 값이 나오면 순차적으로 업데이트 하기 때문에 결측 구간이 길 경우 제대로 imputation이 되지 않은 것을 확인했다.

결측 구간이 길지 않다면 좋은 성능을 보이지만 결측구간이 길다면 다른 모델을 사용해야 한다.