[코드구현] Time Series Forecasting - Informer (AAAI 2021)
한 시간 간격으로 측정 되어 있는 한 달치 특정 구간의 평균 속도 데이터를 이용하여 마지막 일주일 간의 평균 속도를 예측하는 task를 수행해 보았다.
데이터는 도로교통공사의 오픈 데이터를 직접 가공하였으며 아래에서 다운로드할 수 있다.
AAAI 2021 best paper로 선정된 Informer: Beyond Efficient Transformer for Long Sequence Time-Series Forecasting 논문이 구현된 코드를 이용해서 시계열 예측을 진행해 보았다.
논문에 대한 정보는 아래와 같다.
paper: https://arxiv.org/pdf/2012.07436v3.pdf
code: https://github.com/zhouhaoyi/Informer2020
모델에 대해 간단한 설명을 하면 긴시계열 예측에 특화된 transformer기반의 모델이며, Transformer의 긴 길이의 시계열 예측에 대한 문제점 3가지를 해결했다.
전에 블로그에서 번역했었던 논문이다.
AAAI에서 best paper로 선정될 정도면 얼마나 대단할지 궁금해서 논문을 읽었었고 실제로 성능도 확인해 보고 싶어서 실제 코드 적용을 진행했다.
이미 구현되어 있는 코드는 특정 데이터에 대해서만 사용할 수 있었기 때문에 내가 예측을 하고자 하는 교통 데이터에도 적용할 수 있도록 데이터셋 생성, 학습 부분 등 몇몇 부분을 수정했다.
Import Module
# !git clone https://github.com/zhouhaoyi/Informer2020.git
# repository에 있는 models, utils폴더가 있는 곳에서 진행
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import MinMaxScaler
from datetime import timedelta
import torch
from torch import nn
from torch import optim
from torch.utils.data import DataLoader, Dataset
from tqdm import tqdm
# model을 import
from models.model import Informer
필요한 모듈들을 import 한다.
원작자의 레포지토리에서 models, utils폴더만 필요하므로 클론 후 나머지 파일들은 삭제해도 무방하다.
Util function
# standard scler 구현
class StandardScaler():
def __init__(self):
self.mean = 0.
self.std = 1.
def fit(self, data):
self.mean = data.mean(0)
self.std = data.std(0)
def transform(self, data):
mean = torch.from_numpy(self.mean).type_as(data).to(data.device) if torch.is_tensor(data) else self.mean
std = torch.from_numpy(self.std).type_as(data).to(data.device) if torch.is_tensor(data) else self.std
return (data - mean) / std
def inverse_transform(self, data):
mean = torch.from_numpy(self.mean).type_as(data).to(data.device) if torch.is_tensor(data) else self.mean
std = torch.from_numpy(self.std).type_as(data).to(data.device) if torch.is_tensor(data) else self.std
return (data * std) + mean
# 시간 특징을 freq에 따라 추출
def time_features(dates, freq='h'):
dates['month'] = dates.date.apply(lambda row:row.month,1)
dates['day'] = dates.date.apply(lambda row:row.day,1)
dates['weekday'] = dates.date.apply(lambda row:row.weekday(),1)
dates['hour'] = dates.date.apply(lambda row:row.hour,1)
dates['minute'] = dates.date.apply(lambda row:row.minute,1)
dates['minute'] = dates.minute.map(lambda x:x//15)
freq_map = {
'y':[],'m':['month'],'w':['month'],'d':['month','day','weekday'],
'b':['month','day','weekday'],'h':['month','day','weekday','hour'],
't':['month','day','weekday','hour','minute'],
}
return dates[freq_map[freq.lower()]].values
# 한번의 batch를 실행하는 코드
def _process_one_batch(batch_x, batch_y, batch_x_mark, batch_y_mark):
batch_x = batch_x.float().to(device)
batch_y = batch_y.float()
batch_x_mark = batch_x_mark.float().to(device)
batch_y_mark = batch_y_mark.float().to(device)
dec_inp = torch.zeros([batch_y.shape[0], pred_len, batch_y.shape[-1]]).float()
dec_inp = torch.cat([batch_y[:,:label_len,:], dec_inp], dim=1).float().to(device)
outputs = model(batch_x, batch_x_mark, dec_inp, batch_y_mark)
batch_y = batch_y[:,-pred_len:,0:].to(device)
return outputs, batch_y
다른 파일에 이미 구현되어 있던 util 함수들을 약간 수정해서 다시 선언해 주었다.
Make Dataset
class Dataset_Pred(Dataset):
def __init__(self, dataframe, size=None, scale=True):
self.seq_len = size[0]
self.label_len = size[1]
self.pred_len = size[2]
self.dataframe = dataframe
self.scale = scale
self.__read_data__()
def __read_data__(self):
self.scaler = StandardScaler()
df_raw = self.dataframe
df_raw["date"] = pd.to_datetime(df_raw["date"])
delta = df_raw["date"].iloc[1] - df_raw["date"].iloc[0]
if delta>=timedelta(hours=1):
self.freq='h'
else:
self.freq='t'
border1 = 0
border2 = len(df_raw)
cols_data = df_raw.columns[1:]
df_data = df_raw[cols_data]
if self.scale:
self.scaler.fit(df_data.values)
data = self.scaler.transform(df_data.values)
else:
data = df_data.values
tmp_stamp = df_raw[['date']][border1:border2]
tmp_stamp['date'] = pd.to_datetime(tmp_stamp.date)
pred_dates = pd.date_range(tmp_stamp.date.values[-1], periods=self.pred_len+1, freq=self.freq)
df_stamp = pd.DataFrame(columns = ['date'])
df_stamp.date = list(tmp_stamp.date.values) + list(pred_dates[1:])
data_stamp = time_features(df_stamp, freq=self.freq)
self.data_x = data[border1:border2]
self.data_y = data[border1:border2]
self.data_stamp = data_stamp
def __getitem__(self, index):
s_begin = index
s_end = s_begin + self.seq_len
r_begin = s_end - self.label_len
r_end = r_begin + self.label_len + self.pred_len
seq_x = self.data_x[s_begin:s_end]
seq_y = self.data_y[r_begin:r_end]
seq_x_mark = self.data_stamp[s_begin:s_end]
seq_y_mark = self.data_stamp[r_begin:r_end]
return seq_x, seq_y, seq_x_mark, seq_y_mark
def __len__(self):
return len(self.data_x) - self.seq_len- self.pred_len + 1
학습을 진행할 때 필요한 4가지의 변수를 반환하는 Dataset을 생성한다.
input, output, intput의 timestamp, output의 timestamp의 순서대로 값을 반환한다.
모델이 decoder에서 결과를 만들 때 label_len만큼 이전 데이터를 참고한다는 특징이 있어서 input의 길이가 seq_len이고 output의 길이가 pred_len일 때 intput과 output의 형태는 아래와 같다.
0번째 index의 데이터
-
input: [0, seq_len]
-
output: [seq_len - label_len:seq_len + pred_len]
Load Data
data = pd.read_csv("서인천IC-부평IC 평균속도.csv", encoding='CP949')
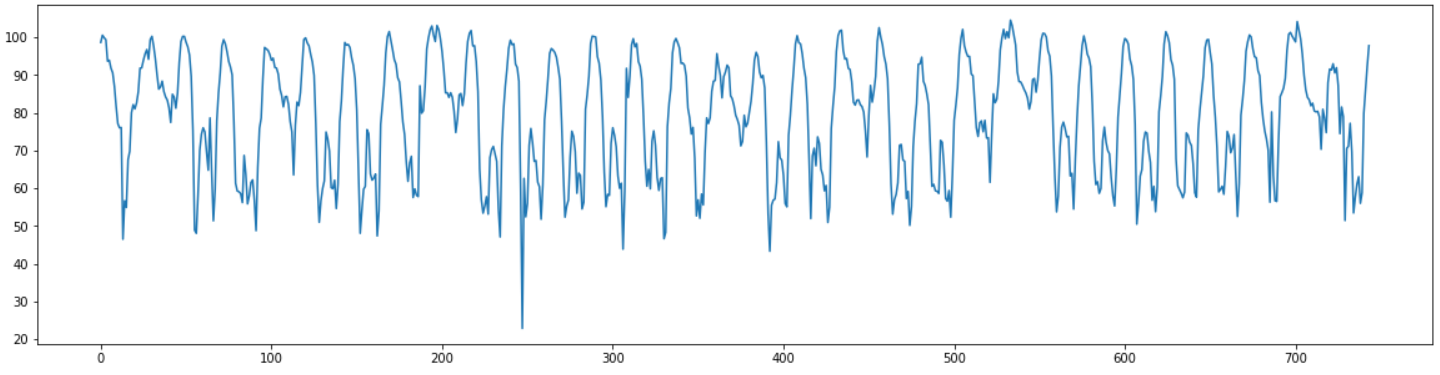
plt.figure(figsize=(20,5))
plt.plot(data["평균속도"])
plt.show()
data.head()
| 집계일시 | 평균속도 | |
|---|---|---|
| 0 | 2021050100 | 98.63 |
| 1 | 2021050101 | 100.53 |
| 2 | 2021050102 | 99.86 |
| 3 | 2021050103 | 99.34 |
| 4 | 2021050104 | 93.64 |
1시간 간격의 평균속도 데이터가 총 744개 존재한다.
data["date"] = data["집계일시"]
data["date"] = data["date"].astype(str)
data["date"] = pd.to_datetime(data["date"].str.slice(start=0, stop=4) + "/" + data["date"].str.slice(start=4, stop=6) + "/" +data["date"].str.slice(start=6, stop=8) + "/" + data["date"].str.slice(start=8, stop=10) + ":0")
data["value"] = data["평균속도"]
min_max_scaler = MinMaxScaler()
data["value"] = min_max_scaler.fit_transform(data["value"].to_numpy().reshape(-1,1)).reshape(-1)
data = data[["date", "value"]]
# 마지막 일주일을 제외한 데이터를 학습 데이터로 사용
data_train = data.iloc[:-24*7].copy()
column의 이름을 date, value로 바꿔주고 date를 datetime 형식으로 변환해준다.
sklearn의 MinMaxScaler를 이용하여 minmax scaling 해준 후 마지막 일주을의 데이터를 제외한 데이터를 최종 학습 데이터로 설정한다.
pred_len = 24*7
seq_len = pred_len#인풋 크기
label_len = pred_len#디코더에서 참고할 크기
pred_len = pred_len#예측할 크기
batch_size = 10
shuffle_flag = True
num_workers = 0
drop_last = True
dataset = Dataset_Pred(dataframe=data_train ,scale=True, size = (seq_len, label_len,pred_len))
data_loader = DataLoader(dataset,batch_size=batch_size,shuffle=shuffle_flag,num_workers=num_workers,drop_last=drop_last)
아까 만든 Dataset class를 이용해서 데이터셋을 생성한다.
seq_len, label_len, pred_len은 모두 24*7로 설정했다.
Train
enc_in = 1
dec_in = 1
c_out = 1
device = torch.device("cuda:1")
model = Informer(enc_in, dec_in, c_out, seq_len, label_len, pred_len, device = device).to(device)
learning_rate = 1e-4
criterion = nn.MSELoss()
model_optim = optim.Adam(model.parameters(), lr=learning_rate)
train_epochs = 100
model.train()
progress = tqdm(range(train_epochs))
for epoch in progress:
train_loss = []
for i, (batch_x,batch_y,batch_x_mark,batch_y_mark) in enumerate(data_loader):
model_optim.zero_grad()
pred, true = _process_one_batch(batch_x, batch_y, batch_x_mark, batch_y_mark)
loss = criterion(pred, true)
train_loss.append(loss.item())
loss.backward()
model_optim.step()
train_loss = np.average(train_loss)
progress.set_description("loss: {:0.6f}".format(train_loss))
loss: 0.040131: 100%|██████████| 100/100 [02:21<00:00, 1.42s/it]
만든 데이터와 Informer 모델을 사용해서 학습을 진행했다.
100번의 epoch로 학습을 진행했다.
Evaluate
학습된 모델을 이용해서 실제 마지막 일주일의 데이터를 예측해 보았다.
scaler = dataset.scaler
df_test = data_train.copy()
df_test["value"] = scaler.transform(df_test["value"])
df_test["date"] = pd.to_datetime(df_test["date"].values)
delta = df_test["date"][1] - df_test["date"][0]
for i in range(pred_len):
df_test = df_test.append({"date":df_test["date"].iloc[-1]+delta}, ignore_index=True)
df_test = df_test.fillna(0)
df_test_x = df_test.iloc[-seq_len-pred_len:-pred_len].copy()
df_test_y = df_test.iloc[-label_len-pred_len:].copy()
df_test_numpy = df_test.to_numpy()[:,1:].astype("float")
test_time_x = time_features(df_test_x, freq=dataset.freq) #인풋 타임 스템프
test_data_x = df_test_numpy[-seq_len-pred_len:-pred_len] #인풋 데이터
test_time_y = time_features(df_test_y, freq=dataset.freq) #아웃풋 타임스템프
test_data_y =df_test_numpy[-label_len-pred_len:]
test_data_y[-pred_len:] = np.zeros_like(test_data_y[-pred_len:]) #예측하는 부분을 0으로 채워준다.
test_time_x = test_time_x
test_time_y = test_time_y
test_data_y = test_data_y.astype(np.float64)
test_data_x = test_data_x.astype(np.float64)
_test = [(test_data_x,test_data_y,test_time_x,test_time_y)]
_test_loader = DataLoader(_test,batch_size=1,shuffle=False)
preds = []
for i, (batch_x,batch_y,batch_x_mark,batch_y_mark) in enumerate(_test_loader):
batch_x = batch_x.float().to(device)
batch_y = batch_y.float().to(device)
batch_x_mark = batch_x_mark.float().to(device)
batch_y_mark = batch_y_mark.float().to(device)
outputs = model(batch_x, batch_x_mark, batch_y, batch_y_mark)
preds = outputs.detach().cpu().numpy()
preds = scaler.inverse_transform(preds[0])
df_test.iloc[-pred_len:, 1:] = preds
예측할 부분의 timestamp를 만들어주고 intput, output데이터를 만들어 준다.
input은 seq_len만큼의 마지막 데이터를 사용하고, output으로는 label_len만큼은 학습 데이터의 마지막 값들, pred_len 만큼은 0으로 padding해서 생성한다.
결과를 얻은 후에는 inverse transform을 시켜준다.
import matplotlib.pyplot as plt
real = data["value"].to_numpy()
result = df_test["value"].iloc[-24*7:].to_numpy()
real = min_max_scaler.inverse_transform(real.reshape(-1,1)).reshape(-1)
result = min_max_scaler.inverse_transform(result.reshape(-1,1)).reshape(-1)
plt.figure(figsize=(20,5))
plt.plot(range(400,744),real[400:], label="real")
plt.plot(range(744-24*7,744),result, label="predict")
plt.legend()
plt.show()
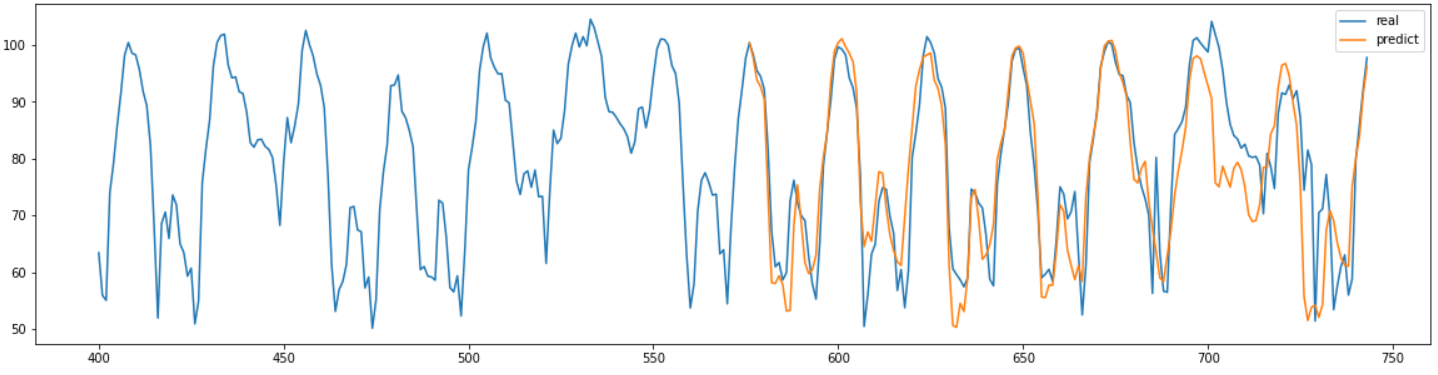
얻은 결과를 그래프로 그려본 결과는 위와 같다.
triaining할 때 test set을 넣은 실수가 있었는지 확인해 볼만큼 비교적 정확하게 결과를 예측한 것을 확인할 수 있었다. 확인해본 결과 정말 training set으로만 예측한 결과였고 상당히 좋은 성능을 가지고 있는 것을 확인할 수 있었다.
def MAPEval(y_pred, y_true):
return np.mean(np.abs((y_true - y_pred) / y_true)) * 100
MAPEval(result, real[-24*7:])
7.752897189847705
결과의 MAPE를 계산해본 결과 약 7.75로 좋은 성능을 가지고 있다는 것을 수치적으로도 확인할 수 있었다.
Conclusion
시계열 예측에 대해 좋은 평가를 받은 최신 논문을 읽고 코드로 구현해 보았다. 그 결과 MAPE 7.75의 좋은 성능을 확인할 수 있었고 시간에 대한 최적화 기법도 도입된 모델이어서 그런지 훈련시간도 다른 DL 모델들에 비해 짧았다.
예전에 자연어 처리에서 많이 사용됐던 RNN 기반 모델들이 최근에는 사용되지 않고 BERT, GPT와 같은 Transformer 기반의 모델들이 주로 사용되고 성능도 훨씬 뛰어난 것으로 알고 있다.
시계열 데이터 처리에서도 조만간 Transformer 기반의 모델들이 기존의 모델들의 성능과 효율성을 앞지르지 않을까라는 생각이 들었다.